Three Squares and Two Ellipses
The applet bellow serves to illustrate the following sangaku [Temple Geometry, pp. 62, 154-155]:
| |
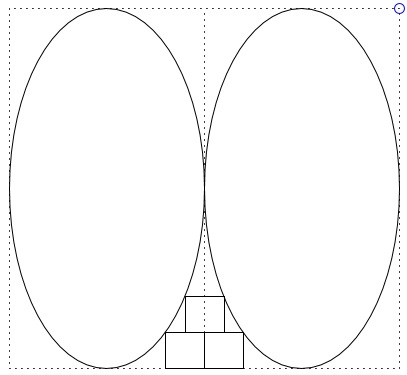
Two congruent ellipses with the major axis 2a and the minor axis 2b touch each other, the minor axis of each passing through the point of contact; l is a common exterior tangent parallel to the minor axis. There are three congruent squares of side t such that two of the squares have a side in common and another side lying on l, and each has a vertex on one of the ellipses, and a third square has a vertex on each ellipse and a side that lies along a side of the first two squares.
Show that
|
| |
|
The problem was carved on an 1838 tablet in the Aichi prefecture. The tablet has since disappeared, but the solution has been discussed in 1976 by H. Fukagawa with a reference to a 1837(!) publication, Chosyu Sinpeki by Tameyuki Yosida. The title translates as Tablets in the Chosyu Prefecture.
Solution
References
H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989
Write to:
Charles Babbage Research Center
P.O. Box 272, St. Norbert Postal Station
Winnipeg, MB
Canada R3V 1L6
Copyright © 1996-2009 Alexander Bogomolny
Solution
The calculations that are necessarily a part of any solution are greatly simplified by an affine trasnformation that squeezes the diagram towards l with coefficient b/a. The horizontal dimensions remain the same, whereas all vertical dimensions are mulitplied by b/a. In particular, the ellipses convert to the circles of radius b and the t×t squares become rectangles t'×t, with t' = tb/a.
In the diagram,
| |
q = b - t', p = b - 2t', u = b - t, v = b - t/2.
|
From
| |
b² = q² + u² = (b - bt/a)² + (b - t)²
|
it follows that
| (1) |
2bt²/a = b² - 2bt(1 + b/a) + t²(1 + b/a)²
|
so that (very clever, I must say)
| (1') |
t √2b/a = b - (1 + b/a)t.
|
Again, from
| |
b² = v² + p² = (b - t/2)² + (b - 2bt/a)²
|
we can deduce that
| (2) |
2bt²/a = b² - 2bt(1/2 + 2b/a) + t²(1/2 + 2b/a)²
|
so that
| (2') |
t √2b/a = b - (1/2 + 2b/a)t.
|
From (1') and (2'),
that is, a = 2b. From (1'), t = a/2 - 3t/2, or 5t = a.
Note: the steps from (1) to (1') and from (2) to (2') are based on unproven assumptions that the right hand sides in (1) and (2) are positive. If they are not, the derivations amount to claiming that 5² = (-5)², say, implies 5 = -5. Which is of course absurd.
Sangaku
- Sangaku: Reflections on the Phenomenon
- Critique of My View and a Response
- 1 + 27 = 12 + 16 Sangaku
- 3-4-5 Triangle by a Kid
- 7 = 2 + 5 Sangaku
- A 49th Degree Challenge
- A Geometric Mean Sangaku
- A Hard but Important Sangaku
- A Restored Sangaku Problem
- A Sangaku: Two Unrelated Circles
- A Sangaku by a Teen
- A Sangaku Follow-Up on an Archimedes' Lemma
- A Sangaku with an Egyptian Attachment
- A Sangaku with Many Circles and Some
- An Old Japanese Theorem
- Archimedes Twins in the Edo Period
- Arithmetic Mean Sangaku
- Bottema Shatters Japan's Seclusion
- Circles and Semicircles in Rectangle
- Circles in a Circular Segment
- Circles Lined on the Legs of a Right Triangle
- Equal Incircles Theorem
- Equilateral Triangle, Straight Line and Tangent Circles
- Equilateral Triangles and Incircles in a Square
- Five Incircles in a Square
- Four Hinged Squares
- Four Incircles in Equilateral Triangle
- Gion Shrine Problem
- Harmonic Mean Sangaku
- Heron's Problem
- In the Wasan Spirit
- Incenters in Cyclic Quadrilateral
- Japanese Art and Mathematics
- Malfatti's Problem
- Maximal Properties of the Pythagorean Relation
- Neuberg Sangaku
- Out of Pentagon Sangaku
- Peacock Tail Sangaku
- Pentagon Proportions Sangaku
- Pythagoras and Vecten Break Japan's Isolation
- Radius of a Circle by Paper Folding
- Review of Sacred Mathematics
- Sangaku à la V. Thebault
- Sangaku and The Egyptian Triangle
- Sangaku in a Square
- Sangaku Iterations, Is it Wasan?
- Sangaku with 8 Circles
- Sangaku with Three Mixtilinear Circles
- Sangaku with Versines
- Sangakus with a Mixtilinear Circle
- Sequences of Touching Circles
- Square and Circle in a Gothic Cupola
- Tangent Circles and an Isosceles Triangle
- The Squinting Eyes Theorem
- Steiner's Sangaku
- Three Incircles In a Right Triangle
- Three Squares and Two Ellipses
- Three Tangent Circles Sangaku
- Triangles, Squares and Areas from Temple Geometry
- Two Arbelos, Two Chains
- Two Circles in an Angle
- Two Sangaku with Equal Incircles
Copyright © 1996-2009 Alexander Bogomolny
|
