Ellipse Touching Sides of Triangle at Midpoints

Cõ Gẫng Lên suggested in a post at the CutTheKnotMath facebook page that the six points on the sides of a triangle equidistant from the respective midpoints lie on an ellipse. The statement below goes a step further, not requiring that all six distances be equal, but only for the points on the same side.

Assume $D,E,F$ are the midpoints of sides $BC,AC,AB$ of $\Delta ABC$. Points $G,H$ on $BC$; $I,J$ on $AC$, and $K,L$ on $AB$ are such that $DG=DH$, $EI=EJ$, $FK=FL$.

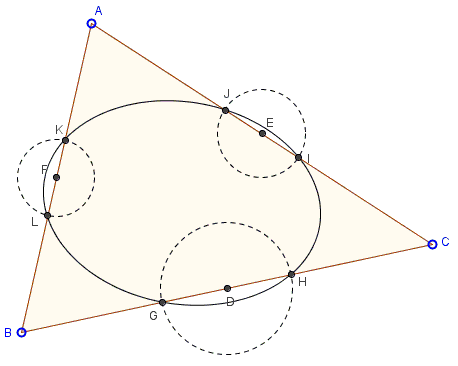
an ellipse in a triangle

There is a unique ellipse through the six points $G,H,I,J,K,L.$ When the points coincide pairwise, the ellipse passes through and is tangent to the midpoints of the $\Delta ABC.$

(The applet below illustrates the configuration.)

Proof

Assume $D,E,F$ are the midpoints of sides $BC,AC,AB$ of $\Delta ABC$. Points $G,H$ on $BC$; $I,J$ on $AC$, and $K,L$ on $AB$ are such that $DG=DH$, $EI=EJ$, $FK=FL$.

an ellipse in a triangle

There is a unique ellipse through the six points $G,H,I,J,K,L.$ When the points coincide pairwise, the ellipse passes through and is tangent to the midpoints of the $\Delta ABC.$

Proof

For a proof, observe that affine transformations do not change the configuration: midpoints remain midpoints (of the sides of the triangle and of, say, segment $GH)$ and an ellipse remains ellipse. (You perform an affine transformation by moving any of the vertices of the triangle in the applet above.) It follows that we may choose a triangle to our liking, while the proof will be still valid in the general case.

So, let's set up a Cartesian coordinates system, with $B$ at the origin, $A(0,2)$ and $C(2,0).$ Then the midpoints also have simple coordinates, $D(1,0),$ $E(1,1)$, $F(0,1)$. For the other six points we have, $G,H=(1\pm h,0)$, $I,J=(1\pm i,1\mp i),$ $K,L=(0,1\pm j).$

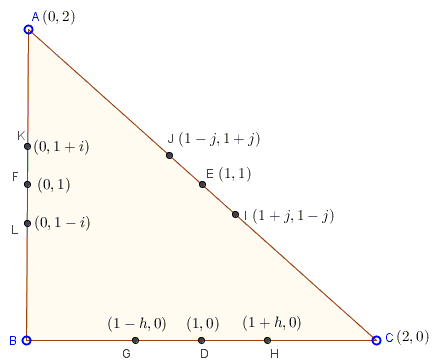
an ellipse in a triangle

We are going to look for a conic (if such exists) through the six points. A conic is given by a second degree equation:

$ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0,$

with only $5$ coefficients independent (because the conic would not change after the equation was divided by one of non-zero coefficients.)

Let's substitute the coordinates of points $G,H,I,J,K,L$ into the equation:

$a(1\pm h)^{2}+2d(1\pm h)+f=0,$
$c(1\pm i)^{2}+2e(1\pm i)+f=0,$
$a(1\pm j)^{2}+2b(1-j^{2})+c(1\mp j)^{2}+2d(1\pm j)+2e(1\mp j)+f=0.$

Unfold the first equation into two:

$a(1+2h+h^{2})+2d(1+h)+f=0,$ and
$a(1-2h+h^{2})+2d(1-h)+f=0.$

Solving these for $a$ and $d$ gives

$\displaystyle a = -d = \frac{f}{h^{2}-1}.$

Similarly, unfolding the second pair of equations, we obtain

$\displaystyle c = -e = \frac{f}{i^{2}-1}.$

Note that $a+d=c+e=0.$

Adding and subtracting the two unfolded equations for $I$ and $J$ gives

$a(1+j^{2})+2b(1-j^{2})+c(1+j^{2})+2d+2e+f=0,$ and
$aj-cj+dj-ej=0,$

the latter of which holds automatically because, as we found, $a+d=c+e=0.$ From the former we can find the remaining coefficient $b$ in terms of $f.$ The six points $G,H,I,J,K,L$ determine a unique ellipse.

The cases we ignored where $h^{2}-1=0,$ or, $i^{2}-1=0,$ or, $j^{2}-1=0,$ correspond to the configurations where some of the points $G,H,I,J,K,L$ coincide with the vertices of the triangle. No ellipse, of cause, can pass through three collinear points.

Now, as $h\rightarrow 0$, $H$ and $G$ move toward $D$ and, at the limit, coincide with the latter. The resulting ellipse becomes tangent to $BC$ at $D$. Letting also $i\rightarrow 0$ and $j\rightarrow 0$ leads to an ellipse tangent to the sides of $\Delta ABC$ at the midpoints. Such ellipse is also unique. I do not see how its uniqueness follows from that of the ellipse through six points. But here is an independent proof.

Let's again make use of affine transformations. Let's preform a transformation (squashing or stretching) that converts one of the ellipses into a circle. In other words, let's assume without loss of generality that in $\Delta ABC$ the incircle is tangent to the sides at the midpoints $D,E,F.$ Let $S$ be the incenter. Then, on one hand, $DS=ES=FS,$ because these are radii of the incircle. Also, say, $BD=CD,$ making right triangles $BDS$ and $CDS$ equal; and the same is true for the other two pairs of right triangles. On the other hand, $BD=BF$ as two tangents from point $B$ to the same circle. It thus follows that all six right triangles are equal, making $\Delta ABC$ equilateral. The question is thus reduced to whether, besides the incircle, there is an ellipse in an equilateral triangle tangent to the midpoints of the sides. The answer is No because by the same device we would be able to convert that ellipse and the equilateral triangle it is inscribed into into a circle inscribed in another equilateral triangles. But an affine transformation (the inverse one) that maps an equilateral triangle onto an equilateral triangle also maps circles onto circles. This ellipse is known as Steiner's inellipse. Its equation in barycentric coordinates has been derived elsewhere.

Note that we chose the hard way to establish the existence of an ellipse tangent to the midpoints of a triangle. An affine transformation of an equilateral triangle onto a given one would map the incircle onto an ellipse immediately resolving the problem of existence. I believe the existence of an ellipse through the six points as discussed above is an independently curious feature.

The ellipse tangent to the midpoints has an exciting property that was designated by Dan Kalman as The Most Marvelous Theorem in Mathematics. The theorem is stated in the complex plane where points are identified with complex numbers:

The roots of the derivative of the polynomial $P(z)=(z-z_{1})(z-z_{2})(z-z_{3})$ are the foci of the ellipse tangent to the midpoints of $\Delta z_{1}z_{2}z_{3}.$

Conic Sections > Ellipse

70530627