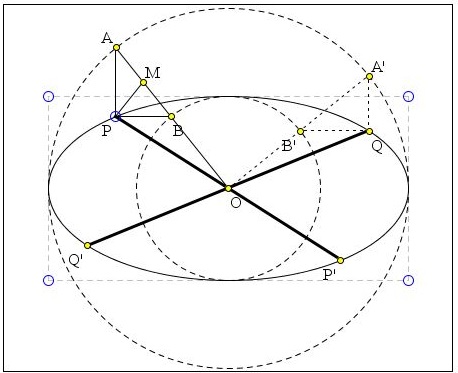
Between Major and Minor Circles

In a polar system of coordinates based at the center of ellipse, an ellipse is presented as a curve

where a and b are the lengths of its half-axes. Consider two circles (one major, the other minor) associated with the ellipse:

Both touch the ellipse at its vertices. If components of a generic point U = (p, q) are denoted p = U_x and q = U_y, we can say that

This explains the configuration illustrated by the applet below.

Since ΔABP is right, the midpoint M of its hypotenuse AB is also the circumcenter: MA = MB = MP. Triangles AMP and BMP are isosceles. By the construction, if O is the center of the ellipse, OA = a, OB = b. It follows that

Let z_X be the complex number associated with a point X. Then arg(z_M) is the angle formed by the radius-vector OM with the (positive) x-axis. For a > b, the angle formed by MP with the (positive) x-axis is -arg(z_M). If z_A = ae^it and z_B = be^it, z_M = (a + b)/2·e^it and

(Euler's formula shows that this is exactly the same as z_P = a cos(t) + ib sin(t), i.e., P = P(t) = (a cos(t), b sin(t)), as expected.)

In an ellipse, conjugate diameters correspond to complementary values of parameter t. The applet illustrates this point too: OA is perpendicular to OA', although PP' and QQ' are not perpendicular, except when they coincide with the axes of the ellipse.

Conic Sections > Ellipse

• What Is Ellipse?
  
• Analog device simulation for drawing ellipses
• Angle Bisectors in Ellipse
• Angle Bisectors in Ellipse II
• Between Major and Minor Circles
• Brianchon in Ellipse
• Butterflies in Ellipse
• Conjugate Diameters in Ellipse
• Dynamic construction of ellipse and other curves
• Ellipse in Arbelos
• Ellipse Between Two Circles
• Euclidean Construction of Center of Ellipse
• Euclidean Construction of Tangent to Ellipse
• Focal Definition of Ellipse
• Focus and Directrix of Ellipse
• From Foci to a Tangent in Ellipse
• Gergonne in Ellipse
• Pascal in Ellipse
• La Hire's Theorem in Ellipse
• Optical Property of Ellipse
• Parallel Chords in Ellipse
• Poncelet Porism in Ellipses
• Reflections in Ellipse
• Three Squares and Two Ellipses
• Three Tangents, Three Chords in Ellipse

Copyright © 1996-2009 Alexander Bogomolny