FJG Capitán's Sangaku
Source
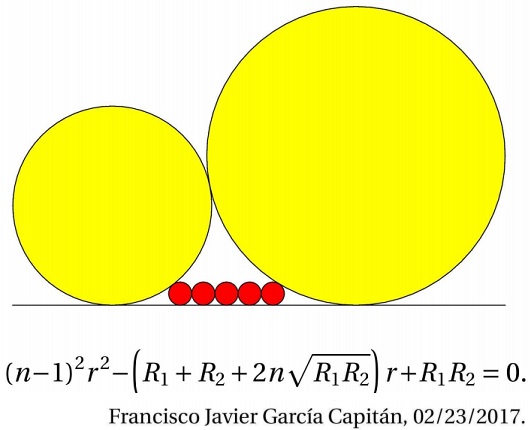
Solution
Assume that the left yellow circle is described by $x^2+(y-R_1)^2=R_1^2;\,$ the right yellow circle by $(x-a)^2+(y-R_2)^2=R_2^2,\,$ $a\gt 0.\,$ The two being externally tangent, we have by the Pythagorean theorem,
$a^2+(R_1-R_2)^2=(R_1+R_2)^2,$
implying $a=2\sqrt{R_1R_2}.\,$ Hence, the right yellow circle is described by $(x-2\sqrt{R_1R_2})^2+(y-R_2)^2=R_2^2.\,$
The rightmost red circle is described by $(x-b)^2+(y-r)^2=r^2.\,$ It being externally tangent to the right yellow circle, we get $(2\sqrt{R_1R_2}-b)^2+(r-R_2)^2=(r+R_2)^2,\,$ implying $b=2\sqrt{R_1R_2}-2\sqrt{rR_2}.$
Similarly, the leftmost red circle has the equation $(x-c)^2+(y-r)^2=r^2,\,$ where $c=2\sqrt{rR_1}.\,$ But $b-c=2(n-1)r\,$ such that $(n-1)r=\sqrt{R_1R_2}-\sqrt{r}(\sqrt{R_1}+\sqrt{R_2}),\,$ i.e., $\sqrt{r}(\sqrt{R_1}+\sqrt{R_2})=\sqrt{R_1R_2}-(n-1)r,\,$ and, by squaring, we obtain
$(n-1)^2r^2-(R_1+R_2+2n\sqrt{R_1R_2})r+R_1R_2=0.$
Acknowledgment
The above problem has been kindly posted by Leo Giugiuc, along with his solution at the CutTheKnotMath facebook page. The problem - by Francisco Javier García Capitán - was originally posted at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73570503
