Two Arbelos, Two Chains

There is a Pappus' chain in arbelos, the shoemaker's knife, and, vacuously, two of them in two cobbler implements. In a particular sangaku documented as 1.8.5 in the collection by Fukagawa and Pedoe the two devices have much on common which induces a relationship between the circles in their chains:

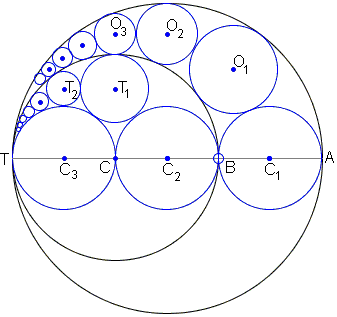
Points T, A, B, C are collinear and AB = BC = CT = 2r. Circles S₁(3r) and S₂(2r) are drawn on AT and BT respectively as diameters. We consider the chain of contact circles O_i(r_i), i = 1, 2, ..., where O₁(r₁) touches C₁(r), drawn on AB as diameter, touches S₁(3r) internally and S₂(2r) externally, and so on. We also use the circles C₂(r) and C₃(r) with respective diameters BC and CT to construct another chain of contact circles T_i(t_i), i = 1, 2, ..., as the figure makes clear. Prove that

t_n / (t_n / r_n - 3) = 2r / 13.

Note that the required identity is likely to be faulty, for it's quite obvious from the construction that t_n < r_n, so that the fraction in the denominator is less the one making the denominator negative and, with it, the whole of the left side. Thus the question is to find a relation in the spirit of the required one.

Solution

t_n / (t_n / r_n - 3) = 2r / 13.

This sangaku is said to be written in 1842 in the Nagano prefecture. The table has since disappeared.

Solution

We make use of a useful formula twice getting, for the small arbelos

t_n = 2r / (n² + 2)

and, for the big one,

r_n = 3r·1/2 / ((n/2)² + 1/2 + 1) = 6r / (n² + 6).

In order to derive at anything resembling 2r/13, we have to somehow get rid of the dependency on n. The easiest way to do that is to pass to the reciprocals:

1 / t_n = (n² + 2) / 2r and
1 / r_n = (n² + 6) / 6r

Obviously,

3 / r_n - 1 / t_n = 4 / 2r = 2 / r,

independent of n. The latter can be rewritten as

1 / r_n · (3 - r_n / t_n) = 2 / r,

r_n / (3 - r_n / t_n) = r / 2.

Perhaps, this is what the tablet was intended for.

Sangaku

71921498