A Sangaku: Two Unrelated Circles

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Chords KN and ST are perpendicular to diameter CP of a circle with center O at points Q and R. SQ intersects the circle in V. (K, S are on one side of CP, N and T on the other. Q is between P and R.) Let q be the radius of the circle inscribed into the curvilinear triangle TQV. Prove that

(1)

1/q = 1/PQ + 1/QR.

Solution

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Solution

The solution comes from an Art of Problem Solving Forum.

For (1) to hold, the radius q must satisfy

(2)

q = PQ·QR / (PQ + QR) = PQ·QR / PR.

So assume a number q is defined by (2). Denote 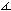QST = 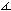QTS = θ. 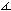Then QN bisects TQV and 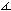NQV = θ. Place point M on QN at distance q/sinθ from Q. A circle with center M and radius q will touch QV in G, such that MG ⊥ QV. We wish to show that this circle is also tangent to the given one, which, for example, will follow from

(3)

OM = r - q,

where r is the radius of the given circle.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Start by applying the Pythagorean theorem in ΔOQM:

OM2= MQ2 + OQ2
 = q2/(sinθ)2 + (PQ - r)2
 = q2 + q2/(tanθ)2 + (PQ - r)2
 = q2 + PQ2·QR2/(PR·tanθ)2 + (PQ - r)2
 = q2 + PQ2·SR2/PR2 + PQ2 - 2r·PQ + r2
 = q2 + PQ2·(SR2 + PR2)/PR2 - 2r·PQ + r2.

By the Intersecting Chords Theorem,

  SR2 = PR·(2r - PR) = 2r·PR - PR2.

Using this we continue:

OM2= MQ2 + OQ2
 = q2 + PQ2·(SR2 + PR2)/PR2 - 2r·PQ + r2
 = q2 + PQ2·2r·/PR - 2r·PQ + r2
 = q2 - 2r·PQ·(PR - PQ)/PR + r2
 = q2 - 2r·PQ·QR/PR + r2
 = q2 - 2r·q + r2
 = (r - q)2,

from which OM = r - q, as expected.

It is noteworthy to observe that the radius in (1) does not depend on the radius r of the given circle, and thus not on point S on the perpendicular PC at R.

Michel Cabart has observed that this problem can be solved by a similar calculation but without first assuming the formula to be true. He proceeds as follows:

We can suppose the circle is of radius 1. Say QP = x, QR = y. Then successively

OQ = 1 - x,
OR = x + y - 1,
QT2 = y2 + [1 - (x + y - 1)2] = 2(x + y) - 2xy - x2,
(sinθ)2 = y2/[ 2(x + y) - 2xy - x2].

By hypothesis OM2 = (1 - q)2 = (1 - x)2 + q2/(sinθ)2.

Move (1 - x)2 to left and divide all by x2q2.

[(1 - q)2 - (1 - x)2]/x2q2= [x - q][2 - (q + x)]/ x2q2 (first member)
 = [2(x + y) - 2xy - x2]/x2y2 (2nd member)

Replace X = 1/x, Y = 1/y, Q = 1/q. First member becomes (Q - X)[2QX - (X + Q)], which by posing Q = X + Y + t becomes

(t + Y) [t(2X - 1) + 2X(X + Y) - 2X - Y] = f(t).

Second member becomes Y[2X(X + Y) - 2X - Y] = f(0).

The trinom f(t) has all its coefficients positive, because

2X - 1 = (2 - x)/x > 0, and
2X(X + Y) - 2X - Y = QT2/x2y2

thus its roots are negative and f(t) is growing when t > 0. So f(t) = f(0) iff t = 0.

A third approach is by Nathan Bowler who starts with the smaller circle:

Take coordinates such that it is the unit circle (q = 1), with Q on the x axis. Let G = (g, h), W = (u, v). Then:

  • QV has equation xg + yh = 1.
  • Q is at (1/g, 0).
  • O is at (1/g, v/ug) = W/ug.
  • V satisfies xg + yh = 1 and (x - 1/g)2 + (y - v/gu)2 = (1 - 1/ug)2.

Further y2 - 2ygv/u + 2g/u - g2 - 1 = 0 so that

QR= -y
 = -gv/u - sqrt(g2/u2 - 2g/u + 1)
 = -gv/u + 1 - g/u
 = 1 - g(1+v)/u.

and

PQ = 1 - 1/ug + v/ug = 1 - (1-v)/ug.

So (PQ - 1)(QR - 1) = (1-v)(1+v)/u2 = 1. Equivalently, 1/PQ + 1/QR = 1 = 1/q.

Related material
Read more...

Mixtilinear Incircles

  • Mixtilinear Circles and Concurrence
  • Radius and Construction of a Mixtilinear Circle
  • Sangaku with Three Mixtilinear Circles
  • Construction and Properties of Mixtilinear Incircles
  • Construction and Properties of Mixtilinear Incircles 2
  • Conic in Mixtilinear Incircles
  • A Sangaku: Two Unrelated Circles

    • Sangaku

    1. Sangaku: Reflections on the Phenomenon
    2. Critique of My View and a Response
    3. 1 + 27 = 12 + 16 Sangaku
    4. 3-4-5 Triangle by a Kid
    5. 7 = 2 + 5 Sangaku
    6. A 49th Degree Challenge
    7. A Geometric Mean Sangaku
    8. A Hard but Important Sangaku
    9. A Restored Sangaku Problem
    10. A Sangaku: Two Unrelated Circles
    11. A Sangaku by a Teen
    12. A Sangaku Follow-Up on an Archimedes' Lemma
    13. A Sangaku with an Egyptian Attachment
    14. A Sangaku with Many Circles and Some
    15. A Sushi Morsel
    16. An Old Japanese Theorem
    17. Archimedes Twins in the Edo Period
    18. Arithmetic Mean Sangaku
    19. Bottema Shatters Japan's Seclusion
    20. Chain of Circles on a Chord
    21. Circles and Semicircles in Rectangle
    22. Circles in a Circular Segment
    23. Circles Lined on the Legs of a Right Triangle
    24. Equal Incircles Theorem
    25. Equilateral Triangle, Straight Line and Tangent Circles
    26. Equilateral Triangles and Incircles in a Square
    27. Five Incircles in a Square
    28. Four Hinged Squares
    29. Four Incircles in Equilateral Triangle
    30. Gion Shrine Problem
    31. Harmonic Mean Sangaku
    32. Heron's Problem
    33. In the Wasan Spirit
    34. Incenters in Cyclic Quadrilateral
    35. Japanese Art and Mathematics
    36. Malfatti's Problem
    37. Maximal Properties of the Pythagorean Relation
    38. Neuberg Sangaku
    39. Out of Pentagon Sangaku
    40. Peacock Tail Sangaku
    41. Pentagon Proportions Sangaku
    42. Proportions in Square
    43. Pythagoras and Vecten Break Japan's Isolation
    44. Radius of a Circle by Paper Folding
    45. Review of Sacred Mathematics
    46. Sangaku à la V. Thebault
    47. Sangaku and The Egyptian Triangle
    48. Sangaku in a Square
    49. Sangaku Iterations, Is it Wasan?
    50. Sangaku with 8 Circles
    51. Sangaku with Angle between a Tangent and a Chord
    52. Sangaku with Quadratic Optimization
    53. Sangaku with Three Mixtilinear Circles
    54. Sangaku with Versines
    55. Sangakus with a Mixtilinear Circle
    56. Sequences of Touching Circles
    57. Square and Circle in a Gothic Cupola
    58. Steiner's Sangaku
    59. Tangent Circles and an Isosceles Triangle
    60. The Squinting Eyes Theorem
    61. Three Incircles In a Right Triangle
    62. Three Squares and Two Ellipses
    63. Three Tangent Circles Sangaku
    64. Triangles, Squares and Areas from Temple Geometry
    65. Two Arbelos, Two Chains
    66. Two Circles in an Angle
    67. Two Sangaku with Equal Incircles
    68. Another Sangaku in Square
    69. Sangaku via Peru
    70. FJG Capitan's Sangaku

    |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    73361645