Sangaku via Peru
Source
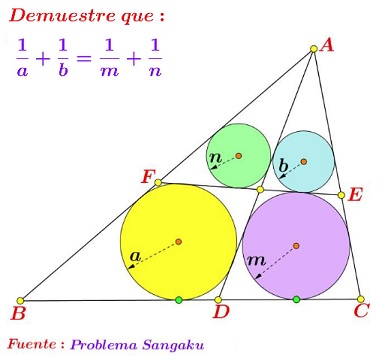
Solution
Let $G\;$ be the point of intersection of $AD\;$ and $EF.\;$ Denote $GE=a_1,\;$ $GF=a_2,\;$ the semiperimeters of triangles $AGE\;$ and $AGF\;$ $p_1\;$ and $p_2,\;$ respectively; $[\Delta AGE]=S_1,\;$ $[\Delta AGF]=S_2.$
The circle $(CDGE)\;$ is $A-$excircle of $\Delta AGE,\;$ implying $\displaystyle\frac{1}{m}=\frac{p_1-a_1}{S_1}.\;$ Similarly, from $(BDGF)\;$ being an excircle of $\Delta AGF,\;$ $\displaystyle\frac{1}{a}=\frac{p_2-a_2}{S_2}.\;$ Clearly, $\displaystyle\frac{1}{b}=\frac{p_1}{S_1}\;$ and $\displaystyle\frac{1}{n}=\frac{p_2}{S_2},\;$ so that $\displaystyle\frac{1}{a}+\frac{1}{b}=\frac{1}{m}+\frac{1}{n}\;$ is equivalent to
$\displaystyle\frac{p_2-a_2}{S_2}+\frac{p_1}{S_1}=\frac{p_1-a_1}{S_1}+\frac{p_2}{S_2},$
which in turn is equivalent to $\displaystyle\frac{a_1}{a_2}=\frac{S_1}{S_2}\;$ which is true.
Acknowledgment
Leo Giugiuc has kindly posted the above problem, with his solution, at the CutTheKnotMath face book page. Leo cam across the problem at a Miguel Ochoa Sanchez's post at the PERU GEOMÉTRICO facebook group.
|Contact| \front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73558931
