A Sushi Morsel

Twice in his books Ross Honsberger discussed the following problem:

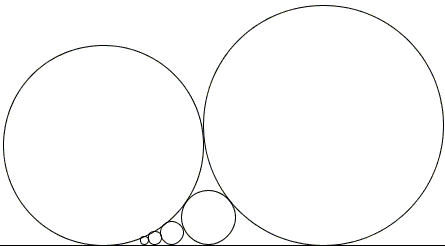
A circle C₀ of radius R₀ = 1 km is tangent to a line L at Z. A circle C₁ of radius 1 mm is drawn tangent to C₀ and L, on the right-hand side of C₀. A family of circles C_i is constructed outwardly to the right side so that each C_i is tangent to C₀, L and the previous circle C_i-1. Eventually the members become so big that it is impossible to enlarge the family further. How many circles can be drawn before this happens?

The first solution in [Gems] is rather a brute force use of coordinate geometry. The second solution [Morsels], which Honsberger attributes to C. Stanley Ogilvy, is based on the observation that, if L is seen as the circle of infinite radius, the problem is reduced to the study of the chain of circles in arbelos or as a particular case of Steiner's chains. The problem is then elegantly reduced to the sequence of circles in a strip of paper by inversion in the circle centered at the point of tangency of C₀ with L and of radius 2R₀.

The earlier discussion comes with no reference; in the later one, Honsberger points to the book Mathematical Games and Pastimes by A. P. Domoryad (Pergamon Press, 1964, problem 19, p. 242).

In a recent article published in The Mathematical Gazette, M. Hajja gives an elementary solution to the problem that makes use of a known result concerning three mutually tangent circles standing on a straight line:

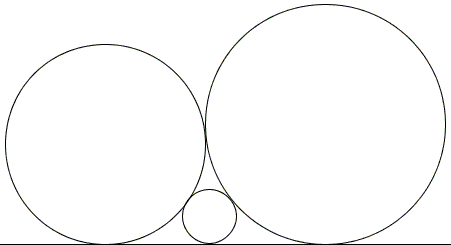
Assuming the radii of the three circles in the diagram are successively R₀, R₁, R₂ we have

(1)	1/√R₂ = 1/√R₁ - 1/√R₀.

By induction, then

(2)	1/√R_n = 1/√R₁ - (n - 1)/√R₀.

Denoting 1/√R_n = u_n, we convert (2) to a simple linear relation

(3)	u_n = u₁ - (n-1)u₀, n > 1.

Since, for all n, u_n > 0, (3) shows that the process may continue as long as u₁ - (n-1)u₀ > 0, o, in other words, while

(4)	n < 1 + u₁ / u₀, i.e, n ≤ u₁ / u₀

For R₀ = 10⁶mm and R₁ = 1 mm, u₁ / u₀ = 10³. Which means that it is impossible to construct circle C₁₀₀₁ and C₁₀₀₀ is the last one, thus solving the problem. (The solution from [Morsels] shows also that R₁₀₀₀ = R₀, giving another reason why the process can't continue beyond n = 1000.)

The point of this note is to observe that the problem and the simple solution above both have a long history. Relation (1) is the subject of an 18th century sangaku. Relation (2) appeared in its generality in a 1789 sangaku and in several modifications during the 19th century. This may be one of those cases where Wasan - the traditional Japanese geometry - beat the West to a punch.

References

M. Hajja, On a Morsel of Ross Honsberger, The Math. Gazette, v. 93, n. 527, July 2009, pp. 309-312
R. Honsberger, Mathematical Gems, MAA, 1973, pp. 52-53, 153-155
R. Honsberger, Mathematical Morsels, MAA, 1978, pp. 218-219

Sangaku

72109842