Angle Bisectors in Ellipse II
Let A and B be two points on an ellipse with foci E and F. The tangents to the ellipse at A and B meet in S. Prove that
| Buy this applet What if applet does not run? |
Conic Sections > Ellipse
- What Is Ellipse?
- Analog device simulation for drawing ellipses
- Angle Bisectors in Ellipse
- Angle Bisectors in Ellipse II
- Between Major and Minor Circles
- Brianchon in Ellipse
- Butterflies in Ellipse
- Concyclic Points of Two Ellipses with Orthogonal Axes
- Conic in Hexagon
- Conjugate Diameters in Ellipse
- Dynamic construction of ellipse and other curves
- Ellipse Between Two Circles
- Ellipse in Arbelos
- Ellipse Touching Sides of Triangle at Midpoints
- Euclidean Construction of Center of Ellipse
- Euclidean Construction of Tangent to Ellipse
- Focal Definition of Ellipse
- Focus and Directrix of Ellipse
- From Foci to a Tangent in Ellipse
- Gergonne in Ellipse
- Pascal in Ellipse
- La Hire's Theorem in Ellipse
- Maximum Perimeter Property of the Incircle
- Optical Property of Ellipse
- Parallel Chords in Ellipse
- Poncelet Porism in Ellipses
- Reflections in Ellipse
- Three Squares and Two Ellipses
- Three Tangents, Three Chords in Ellipse
- Van Schooten's Locus Problem
- Two Circles, Ellipse, and Parallel Lines
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015Alexander Bogomolny
Let A and B be two points on an ellipse with foci E and F. The tangents to the ellipse at A and B meet in S. Prove that
Proof
To see why this is so, draw an ellipse through S confocal to the given one. This remids of the configuration which showed the ellipse as an envelope of a family of straight lines.
| Buy this applet What if applet does not run? |
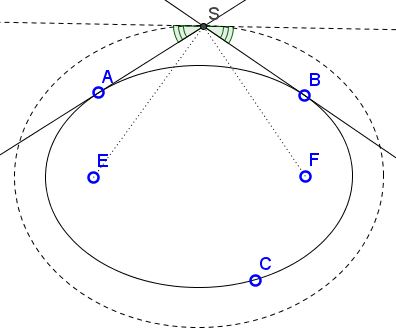
So we now have two confocal ellipses: ellipse1 (the original one) and ellipse2 (passing through S.) The configuration admits the following interpretation. Draw a tangent to ellipse1 at A till it hits ellipse2 in S. Reflect it at S and continue to the next intersection with ellipse2, and so on. All so constructed lines will touch an ellipse confocal with ellipse2 which is bound to be ellipse1 since the latter, by the construction, is already tangent to the first line AS. It follows that the second line in the chain is necessarily BS, implying that AS and BS are equally inclined to the tangent to ellipse2 at S. But so are ES and FS, and we are done.
Conic Sections > Ellipse
- What Is Ellipse?
- Analog device simulation for drawing ellipses
- Angle Bisectors in Ellipse
- Angle Bisectors in Ellipse II
- Between Major and Minor Circles
- Brianchon in Ellipse
- Butterflies in Ellipse
- Concyclic Points of Two Ellipses with Orthogonal Axes
- Conic in Hexagon
- Conjugate Diameters in Ellipse
- Dynamic construction of ellipse and other curves
- Ellipse Between Two Circles
- Ellipse in Arbelos
- Ellipse Touching Sides of Triangle at Midpoints
- Euclidean Construction of Center of Ellipse
- Euclidean Construction of Tangent to Ellipse
- Focal Definition of Ellipse
- Focus and Directrix of Ellipse
- From Foci to a Tangent in Ellipse
- Gergonne in Ellipse
- Pascal in Ellipse
- La Hire's Theorem in Ellipse
- Maximum Perimeter Property of the Incircle
- Optical Property of Ellipse
- Parallel Chords in Ellipse
- Poncelet Porism in Ellipses
- Reflections in Ellipse
- Three Squares and Two Ellipses
- Three Tangents, Three Chords in Ellipse
- Van Schooten's Locus Problem
- Two Circles, Ellipse, and Parallel Lines
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015Alexander Bogomolny
| 49552218 |
