Sangaku and The Egyptian Triangle

 

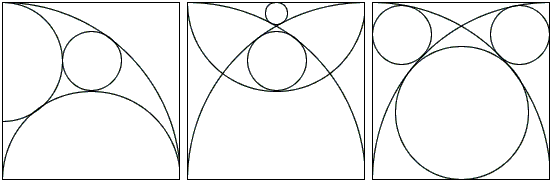
Three sangaku that require to determine the relative radii of the circles shown can be solved by a direct application of the Pythagorean theorem, see below, but if combined into a single (and a little amplified, sangaku-ready) configuration

 

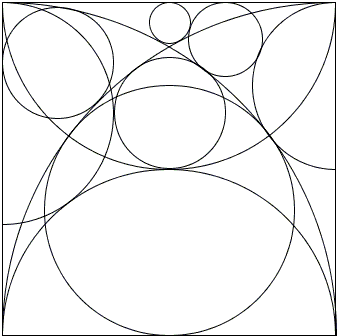
reveal existence of possible relationships not obvious when they are studied separately. The configuration in fact, as was noted by L. Bankoff and C. W. Trigg quarter of a century before sangaku grew in popularity after a 1998 Scientific American article, is rich with surprises, the main being the numerous sightings of the famous 3:4:5 triangle.

 

The latter is most often referred to as the Rope-stretchers triangle and sometimes as the Egyptian triangle. (Both because of the belief that this simplest of the Pythagorean triangles was used by the ancient rope-stretchers in construction and, in particular, in construction of the Great Pyramids. Sometimes, however, the term Egyptian triangle is preserved for the one related to the dimensions of the pyramid of Cheops and the golden ratio.)

 

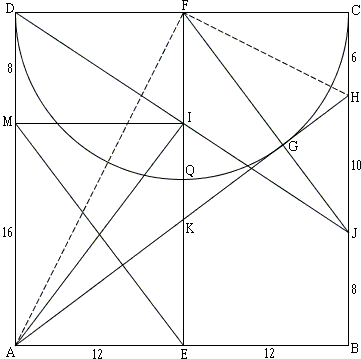
For convenience, assume the side of the square is 24 so that DF = FC = 12. Also, for simplicity, a circle with center X say, will be denoted (X). AH is tangent to (F) in G. Thus also FG = 12. The radius FG extends to meet BC in J and is perpendicular to AH.

HC = HG as tangents to (F) from H. For the same reason AG = AD = 24. FH bisects ∠CFG and FA bisects its supplementary angle ∠DFG.

From here, ∠AFH = 90° and FG is the altitude to the hypotenuse of right ΔAFH. We, therefore, have FG2 = AG·GH, or 122 = 24·GH. Wherefrom GH = 6 and so HC = 6.

Then HB = 18, AH = 30, AK = 15, KG = 9, EK = 9, FK = 15, QK = 3, CJ = 16, FI = 8, EI = 16, AI = 20 (by the Pythagorean theorem), HJ = 10 ( ΔFGK is similar to ΔJGH), BJ = 8, GJ = 8, FJ = 20, IQ = 4.

We see that triangles FCJ, HGJ, FGK, AKE, AEI, AEM, and ABH are all 3:4:5 triangles.

 

Let T be the intersection of AI extended with (A). Then AT = 24 and, since AI = 20, IT = 4 = IQ. Which says that the circle (I) of radius 4 is tangent to (A), (B), (F), and (E). If we extend AT further and let R on AT be on the vertical tangent SR to (I), then, for one, ΔIRS is similar to AEI and, hence, is also 3:4:5. Since IS = IQ = 4, IR = 20/3, SR = 16/3, RT = 8/3. If U is the intersection of SR and CD, then

  RU = FI - SR = 8 - 16/3 = 8/3 = RT.

In addition, if V is on BC and VC = RU, then VH = 10/3, RV = 8 and, by the Pythagorean theorem, HR = 26/3, so that again RX = 8/3. It follows that the circle (R) with radius 8/3 is tangent to (A), (I), (H) and CD. As an extra, it is also tangent to (W) with radius 3/2. ΔHVR is 5:12:13. The right triangle with vertical and horizontal legs and hypotenuse RW is 7:24:25.

References

  1. L. Bankoff, C. W. Trigg, The Ubiquitous 3:4:5 Triangle, Math Magazine, v 47, n 2 (Mar., 1974), pp. 61-70

  2. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

    Write to:

    Charles Babbage Research Center
    P.O. Box 272, St. Norbert Postal Station
    Winnipeg, MB
    Canada R3V 1L6

Sangaku

  1. Sangaku: Reflections on the Phenomenon
  2. Critique of My View and a Response
  3. 1 + 27 = 12 + 16 Sangaku
  4. 3-4-5 Triangle by a Kid
  5. 7 = 2 + 5 Sangaku
  6. A 49th Degree Challenge
  7. A Geometric Mean Sangaku
  8. A Hard but Important Sangaku
  9. A Restored Sangaku Problem
  10. A Sangaku: Two Unrelated Circles
  11. A Sangaku by a Teen
  12. A Sangaku Follow-Up on an Archimedes' Lemma
  13. A Sangaku with an Egyptian Attachment
  14. A Sangaku with Many Circles and Some
  15. A Sushi Morsel
  16. An Old Japanese Theorem
  17. Archimedes Twins in the Edo Period
  18. Arithmetic Mean Sangaku
  19. Bottema Shatters Japan's Seclusion
  20. Chain of Circles on a Chord
  21. Circles and Semicircles in Rectangle
  22. Circles in a Circular Segment
  23. Circles Lined on the Legs of a Right Triangle
  24. Equal Incircles Theorem
  25. Equilateral Triangle, Straight Line and Tangent Circles
  26. Equilateral Triangles and Incircles in a Square
  27. Five Incircles in a Square
  28. Four Hinged Squares
  29. Four Incircles in Equilateral Triangle
  30. Gion Shrine Problem
  31. Harmonic Mean Sangaku
  32. Heron's Problem
  33. In the Wasan Spirit
  34. Incenters in Cyclic Quadrilateral
  35. Japanese Art and Mathematics
  36. Malfatti's Problem
  37. Maximal Properties of the Pythagorean Relation
  38. Neuberg Sangaku
  39. Out of Pentagon Sangaku
  40. Peacock Tail Sangaku
  41. Pentagon Proportions Sangaku
  42. Proportions in Square
  43. Pythagoras and Vecten Break Japan's Isolation
  44. Radius of a Circle by Paper Folding
  45. Review of Sacred Mathematics
  46. Sangaku à la V. Thebault
  47. Sangaku and The Egyptian Triangle
  48. Sangaku in a Square
  49. Sangaku Iterations, Is it Wasan?
  50. Sangaku with 8 Circles
  51. Sangaku with Angle between a Tangent and a Chord
  52. Sangaku with Quadratic Optimization
  53. Sangaku with Three Mixtilinear Circles
  54. Sangaku with Versines
  55. Sangakus with a Mixtilinear Circle
  56. Sequences of Touching Circles
  57. Square and Circle in a Gothic Cupola
  58. Steiner's Sangaku
  59. Tangent Circles and an Isosceles Triangle
  60. The Squinting Eyes Theorem
  61. Three Incircles In a Right Triangle
  62. Three Squares and Two Ellipses
  63. Three Tangent Circles Sangaku
  64. Triangles, Squares and Areas from Temple Geometry
  65. Two Arbelos, Two Chains
  66. Two Circles in an Angle
  67. Two Sangaku with Equal Incircles
  68. Another Sangaku in Square
  69. Sangaku via Peru
  70. FJG Capitan's Sangaku

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny

Let's, for example find the radius of (K) tangent to (A), (B) and AB. Actually we already saw that KE = KG = 9. If we wish to employ the Pythagorean theorem in ΔAEK, then denoting the radius of (K) as r we'll have

  (24 - r)2 - r2 = 122,

which gives

  576 - 48r = 144, or
48r = 432,
r = 9.

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny

72104555