Various Geometries

The term "Non-Euclidean Geometries" usually applies to the geometries of Riemann and Lobachevsky. However, once Euclid's postulates have been lowered from their lofty, 2300 years old pedestal, and brought into active mathematical investigation, many more geometries had evolved. Under close scrutiny, it became apparent that Euclid's Elements are not as solidly based on his postulates as one might have expected of the treatise known as the Mathematical Bible. Omissions were fundamental. For example, the first postulate

A straight line may be drawn between any two points.

would be true even if there were no points. For, as we know, falsity implies anything. We may stipulate that there are 2, 3, 4 point geometries.

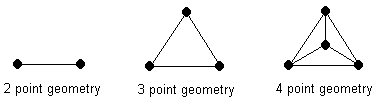
Note that line segments that appear on the diagrams are not elements of those geometries. They are there only to indicate the lines that pass through certain points. In the 2 point geometry, there exists a single line that contains exactly 2 points. (Without rigorous axiomatization, one may insist that, in addition, there are also two 1 point lines.) In the 4 point geometry, with additional stipulation that a line contains exactly two points we even have the Fifth postulate as annunciated by Euclid.

From this examples, another Euclid's omission becomes apparent. Unless stipulated otherwise, a line can contain two distinct points without having points in-between. The boy who could not prove that a line can't intersect three sides of a triangle in their interior points, raised a deep question overlooked by generations of professionals.

More comprehensive axiomatic systems had been developed by G. Peano (1889), D. Hilbert (1899), and O. Veblen (1904) who filled in the logical gaps left by Euclid in his Elements. The updates incorporate axioms of Order, Congruence, and Continuity. Euclid's half-intuitive, half-formalized Common Notions are directly included into the axiomatic system. In the following, I shall nonetheless relate to the set of Postulates as they appear in Elements.

Another approach to defining and classifying various geometries was introduced, in 1872, by Felix Klein (1849-1925) in the inaugural address he gave upon appointment to the Faculty and Senate of the University of Erlanger. The approach became known as the Erlanger Programm.

To prove I.4 (SAS) and I.8 (SSS), Euclid allows superposition of figures. Superposition is achieved by transforming one triangle onto another. Euclid implicitly assumed that geometric figures do not change by rigid motions. Rigid motions (e.g., translation, rotation, reflection) form an algebraic structure known as a group. Put another way, in Euclid's geometry, some properties of figures (lengths, angles, areas) remain invariant under the group of rigid motions. As Klein showed, other (although not all) geometries can be characterized by various groups of transformations. Since then, study of particular kinds of transformations became an integral part of geometric research and development.

On this page, for the reference sake, I shall collect short Descriptions of and facts from various geometries as they become necessary for other discussions. In time, the page will serve as an index for more detailed coverage.

Absolute Geometry

The term Absolute Geometry had been introduced by J.Bolyai in 1832. Absolute Geometry is derived from the first four of Euclid's postulates. The first 28 Propositions from Elements, I belong to Absolute Geometry. Euclid apparently made a conscientious effort to see how far he can reach without invoking his Fifth postulate. All theorems of Absolute Geometry are automatically true in the geometries of Euclid, Lobachevsky and Riemann since those three only differ in their treatment of the Fifth postulate. For example (Elements, I.15),

If two straight lines cut one another, they make the vertical angles equal to one another.

is true in all three rival geometries.

Affine Geometry

Affine Geometry is not concerned with the notions of circle, angle and distance. It's a known dictum that in Affine Geometry all triangles are the same. In this context, the word affine was first used by Euler (affinis). In modern parlance, Affine Geometry is a study of properties of geometric objects that remain invariant under affine transformations (mappings).

Affine transformations preserve collinearity of points: if three points belong to the same straight line, their images under affine transformations also belong to the same line and, in addition, the middle point remains between the other two points. As further examples, under affine transformations

parallel lines remain parallel,
concurrent lines remain concurrent (images of intersecting lines intersect),
the ratio of length of line segments of a given line remains constant,
the ratio of areas of two triangles remains constant (and hence the ratio of any areas remain constant),
ellipses remain ellipses and the same is true for parabolas and hyperbolas.
barycenters of triangles (and other shapes) map into the corresponding barycenters

Analytically, affine transformations are represented in the matrix form f(x) = Ax + b, where the determinant det(A) of a square matrix A is not 0. In a plane, the matrix is 2×2; in the space, it is 3×3. One way to arrive at the matrix representation is to select two points (two origins) and associate with each an appropriate number of independent vectors (2 in the plane, 3 in the space), to form an affine basis. b is then the translation that maps one of the selected points onto another. In particular, affine transformations that preserve a point are of the form f(x) = Ax. Each basis defines a system of coordinates. Point f(x) has the same coordinates in the second system as x has in the first. Coordinates of f(x) in the first system are exactly defined by the matrix form: f(x) = Ax + b.

Quite often (for example, in Computer Graphics) an additional coordinate is appended which allows writing f(x) = Ax + b in a more compact form. For instance, let n = 2. Replace

with

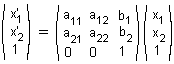
From here, it is just one step to the homogeneous coordinates which play an important role in Projective Geometry.

Affine transformations can also be defined in terms of barycentric coordinates. Choose two arbitrary triangles and associate with each a system of barycentric coordinates. Allowing for negative values as well, any triple of real numbers u, v, w that satisfies u + v + w = 1, represents one point associated with one triangle and another associated with the second triangle. Such an association of barycentric coordinates leads to an affine transformation under which vertices of one triangle correspond to vertices of the other which, in particular, explains the dictum at the beginning of this section.

Projective Geometry

Projective Geometry originated in the works of Désargues (1593-1662), B.Pascal, G.Monge (1746-1818) and was further developed in the 19th century by J.V.Poncelet (1788-1867) and C.J.Brianchon (1785-1864). Intuitively, Projective Geometry of a plane starts in a three dimensional space.

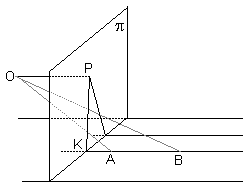
Select a point O (Observer) and a plane of observation π (the vertical plane in the diagram.) The selected plane π is a starting point for a model of Projective Geometry. Points on that plane are associated with straight lines through point O. (Incidentally, the set of all lines through a given point is called a pencil of lines. The set of all planes through a point is called a bundle of planes.)

Planes through O become straight lines in the projective plane. Lines that intersect plane π (like AB) project into straight lines (KP in the diagram.) A fundamental fact about this correspondence is that the image of any other straight line parallel to AB will pass through the point P. P is known as the vanishing point in the direction defined by AB.

There is one caveat though. The plane through O parallel to π and all the lines in that plane have no (projective) images on π. However, internally, elements of a pencil are indistinguishable. Only after the observation plane is selected, there appears one plane (and the lines that belong to it) that is discriminated against.

By definition, Projective Plane is a pencil of straight lines and a bundle of planes through the same point. When modeled with a projective mapping as above, the plane of the bundle parallel to the observation plane, is called the line at infinity. Each line in the pencil parallel to the observation plane defines a point at infinity. Parallel lines define the same point at infinity which , naturally, belongs to the line at infinity. Lines in the projective plane all pass through a point at infinity defined by their direction. Therefore, in Projective Geometry, any two lines intersect. Some intersect at the finite part of the plane, some (that share a direction) intersect at a point in infinity. Let me repeat that the distinction between the two cases only appears when a 3-dimensional pencil of lines (which is the 2-dimensional Projective Plane) is modeled as an ordinary 2-dimensional plane.

Analytically, Projective Plane is defined with homogeneous coordinates. This is done in the following way.

Assume O is placed at the origin of some coordinate system consisting of three vectors e, f, and g. Any other vector n can be expressed as a combination n = ue+ vf + wg. If n meets plane π at a point N then (u,v,w) are called the homogeneous coordinates of the point N. The coordinates are homogeneous because they are defined up to a constant multiple. Indeed, two vectors n and tn have the same direction and, therefore, define the same point N. The triple (tu,tv,tw) defines exactly the same point as the triple (u,v,w). In homogeneous coordinates, projective transformations appear as

(1)

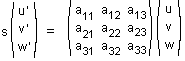
where coefficient s is arbitrary due to homogeneity of the coordinate. u',v', and w' are coordinates of the transformed point.

Two triples of vectors e₁, f₁, and g₁ and e₂, f₂, and g₂ define the same set of homogeneous coordinates in π iff they are proportional, or homothetic: there exists a real number h such that simultaneously

(2)	e₂ = he₁, f₂ = hf₁, and g₂ = hg₁.

Another way to express (1) is to assert that their barycentric directions e₁ + f₁ + g₁ and e₂ + f₂ + g₂ are also proportional (and, therefore, define the same point in the plane π.)

On the other hand, given three independent directions through O, we may vary relative lengths of vectors along these directions so that their barycentric line will pierce the plane π in an arbitrarily selected point. From here we obtain the Projective Geometry dictum, in Projective Geometry all quadrilaterals are the same. Projective mappings are thus defined by arbitrary 4 points in the plane π no three of which are collinear.

More accurately and in the manner similar to the definition of affine mappings in the barycentric coordinates, we first choose three noncollinear points A,B, and C. This establishes three directions e, f, and g through the point O. Next we fix the desired barycenter D inside (or outside if weights are allowed to be negative) ΔABC. Selection of the barycenter D is equivalent to adjusting the lengths of vectors e, f, and g which, in turn, is equivalent to placing some weights at points A,B, and C. Four points A,B,C,D uniquely define a set of homogeneous coordinates in π. Two sets of homogeneous coordinates in π define a projective mapping of π by relating points with the same coordinates in the two systems.

Projective transformations preserve collinearity and the cross-ratio of collinear points.

1-Dimensional Projective Geometry

By analogy with the 3-dimensional case, a (planar) pencil of lines is the set of lines in the same plane that pass through the same point. 1-dimensional Projective Geometry which is defined as a planar pencil of lines is modeled by an ordinary straight line in the following manner. In a plane, fix a point O and consider a pencil of lines through O. Choose a line π that does not belong to the pencil. All lines of the pencil but one intersect π. This establishes a correspondence between the lines of the pencils and points of the line π. The line of the pencil parallel to π is called the point at infinity. The line π augmented with the point at infinity is known as the extended line.

Homogeneous coordinates (u,v) are introduced in the same manner as in the 2-dimensional case above. By analogy with (1), projective transformations are defined analytically by

(3)

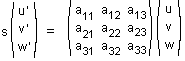
Writing (3) explicitly we get

(4)	su' = a₁₁u + a₁₂v sv' = a₂₁u + a₂₂v

which reduces to u'/v' = (a₁₁u + a₁₂v)/(a₂₁u + a₂₂v). Finally, with u/v replaced by x, x' = (a₁₁x + a₁₂)/(a₂₁x + a₂₂). Functions in the form

f(x) = (ax + b)/(cx + d)

have been studied by A.F.Möbius (1790-1868) and are known as the Möbius Transformations. For x = -d/c (provided c ≠ 0) f(x) is taken to be the point at infinity introduced earlier. For x being the point at infinity, f(x) = a/c (with the same caveat.) For c = 0, f(x) turns out to be a simpler, linear transformation f(x) = ax + b which maps the point at infinity on itself. This is also the most general form of the 1-dimensional affine transformation. If the line is considered as 1-dimensional Affine Geometry, the point at infinity is known as its ideal element. Affine Line extended with its ideal element serves as a model for 1-dimensional Projective Geometry. Projective Geometry differs from its extended Affine counterpart in that it makes no distinction between ordinary and ideal elements. 1-dimensional Projective Geometry with one point marked, is modeled by the extended line. Projective mappings that leave the marked point fixed, if restricted to the line without the point, represent affine mappings of the unextended line π.

A similar situations exists in all other dimensions. For n = 2, the affine plane π extended with an ideal line (the line at infinity) models Projective Plane. Projective mappings that leave one line fixed, correspond to affine mappings of the unextended plane. Since, for n=2, one ideal point is associated with a pencil of parallel lines, this point is reached regardless which direction one moves on the line. Replacing a plane with an open disk, one ideal element will correspond to two opposite points of the circle. When the two points in each pair are identified, one obtains the crosscap representation of the Projective Plane.

For n=2, homogeneous coordinates are uniquely defined by a selection of 4 points. Each such selection uniquely defines a projective mapping to a projective plane with a second fixed quadruple of points. In terms of a pencil through a point 0, projective transformations are uniquely defined by four elements of the pencil.

For n=1, projective mappings are uniquely defined by images of three (planar) pencil elements.

71871394