Butterflies in Ellipse: What is it about?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander BogomolnyButterflies in Ellipse
The applet below provides another perspective on the Two Butterflies theorem and the porism observed by Nathan Bowler. The theorem states this: given a cyclic quadrilateral inscribed in a circle, a line (not necessarily crossing the circle) and four points on the line in which the sides of the quadrilateral cross the line. For any other quadrilateral inscribed in the circle, if three of its sides pass through any three (of the above four) points on the line, then the fourth side passes through the fourth point. Number 4 in the statement can be replaced with any even number.
Furthermore, since the theorem only deals with incidences of points and line, it is of projective character and must hold for any non-degenerate conic. The applet below illustrates the theorem for ellipses.
| Buy this applet What if applet does not run? |
We want two prove the following theorem:
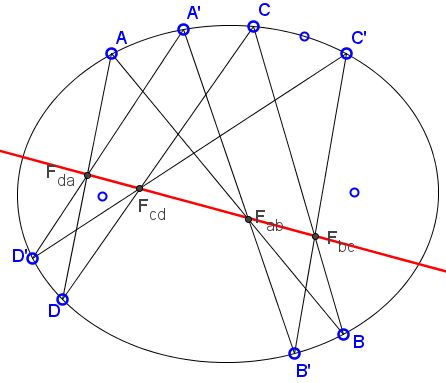
Let there be two quadrilaterals ABCD and A'B'C'D' inscribed into a conic such that the sides DA, AB, BC, CD of the former pass through collinear points Fda, Fab, Fbc, Fcd. If the sides D'A', A'B', B'C' meet the same line L in Fda, Fab, Fbc then the fourth sides C'D' meets L in Fcd.
Proof
|
Consider the cyclic hexagon ABCA'B'C'. Its opposite sides AB and A'B' meet in Fab and the sides BC and B'C' meet in Fbc. By Pascal's theorem the third pair of lines, AC and A'C' meet in a point P collinear with Fab and Fbc, i.e. lying on line L.
Now, consider the hexagon ADCA'D'C'. The sides AC and A'C' meet in P on L; the sides CD and C'D' meet in Fcd on L. Therefore, the sides AD and A'D' meet in a point on L. But AD passes through Fda on L. Hence, so does A'D' and we are done.
Given its projective character, it is not surprising that the theorem follows from Pascal's theorem. Perhaps surprisingly, the reverse is also true: we may derive Pascal's theorem from the statement of quadrilaterals.
Let the hexagon ABCDEF be inscribed in a conic, let AB meet DE in P, BC meet EF in Q, CD meet PQ in R and let AD meet PQ in T. Observe two quadrilaterals ABCD and DEFA. Their sides meet in pairs: AB and DE in P, BC and EF in Q, and their common side AD passes through T. By the definition of T, the three points P, Q, T are collinear. By the theorem just proved, line AF passes through the intersection of CD and PQ, i.e., point R. This proves Pascal's theorem.
The proof that the porism holds for a 2k-gon, k ≥ 2 is by induction, along the same lines as above.
References
- D. Jones, Quadrangles, Butterflies, Pascal's Hexagon, and Projective Fixed Points, Amer Math Monthly 87, no 3 (Mar., 1980), 197-200
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny| 49552103 |
