An Extension of a Sangaku with Touching Circles
Source
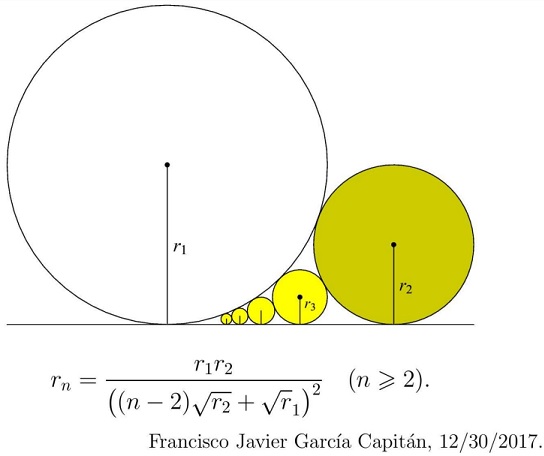
Solution 1
We rewrite the problem in the form $\displaystyle \frac{1}{\sqrt{r_n}}=\frac{n-2}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}$ and, for a proof, use the induction on the number $n$ of the circles.
For $n=3,$ this is the subject of an earlier Sangaku.
Assume the statement holds for $n=k\ge 3,$ which we'll write as $\displaystyle \frac{1}{\sqrt{r_k}}=\frac{k-2}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}.$ Let's prove it for $n=k+1.$
From the basic step,
$\displaystyle\begin{align}\frac{1}{\sqrt{r_{k+1}}}&=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_k}}\\ &=\frac{1}{\sqrt{r_1}}+\left(\frac{k-2}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}\right)\\ &=\frac{k-1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}, \end{align}$
which is the required identity.
Solution 2
For two touching circles with radii $R$ and $r$ such that $R\geq r$, let the angle made by the line through the centers of the circles with the horizontal be $\phi(R,r)$. Thus,
$\displaystyle\sin\phi(R,r)=\frac{R-r}{R+r} \Rightarrow \cos\phi(R,r)=2\frac{\sqrt{rR}}{R+r}.$
Consider the three circles with radii $r_1$, $r_{n-1}$, and $r_n$. Applying the constraint for the horizontal distance between the centers,
$\begin{align} (r_1+r_{n-1})\cos\phi(r_1,r_{n-1})&=(r_1+r_n)\cos\phi(r_1,r_n)+(r_{n-1}+r_n)\cos\phi(r_{n-1},r_n) \\ \Rightarrow \sqrt{r_1r_{n-1}}&=\sqrt{r_1r_n}+\sqrt{r_{n-1}r_n} \\ \Rightarrow \frac{1}{\sqrt{r_n}}&=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_{n-1}}}. \end{align}$
Thus,
$\displaystyle\begin{align} &\frac{1}{\sqrt{r_3}}=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}, \\ &\frac{1}{\sqrt{r_4}}=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_3}} =\frac{2}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}, \\ &\frac{1}{\sqrt{r_5}}=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_4}} =\frac{3}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}, \\ &\ldots \\ &\frac{1}{\sqrt{r_n}}=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_{n-1}}} =\frac{(n-2)}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}. \end{align}$Re-arranging the last expression,
$\displaystyle r_n=\frac{r_1r_2}{\left[(n-2)\sqrt{r_2}+\sqrt{r_1}\right]^2}.$
Acknowledgment
This problem has been posted by Francisco Javier García Capitán at the Peru Geometrico facebook groop. Leo Giugiuc has kindly communicated to me the problem as the New Year present, along with his solution. Solution 2 is by Amit Itagi.
The problem is a generalization of a Sangaku from the Miyagai prefecture.
- An Extension of a Sangaku with Touching Circles
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579925
