A Sangaku with Many Circles and Some: What Is This About?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The applet purports to suggest the following 1837 sangaku [Temple Geometry, 1.5.7] from the Aichi prefecture:

|
|
AB is a diameter of O(r) and forms two semicircles. In one of these the equal circles O1(r1) and O'1(r1) touch AB and also O(r) internally. The circles O2(r1) and O'2(r1) are mirror images of these two circles in AB. The circle O(r3) touches the 4 circles we have just described externally, and the circle O4(r4) touches O1(r1) and O'1(r1) externally and O(r) internally. Show that
In the particular case where r3 = r/9, show that
where O5(r5) has interior contact, as shown, with both O1(r1) and O'1(r1). |
We'll proceed a step at a time. First, let X be the points of contact of O1(r1) with AB and x = OX.

|
By the Pythagorean theorem,
| (r - r1)² = x² + (r1)². |
From which
| (1) | r1 = (r² - x²) / 2r. |
Next we find r3:
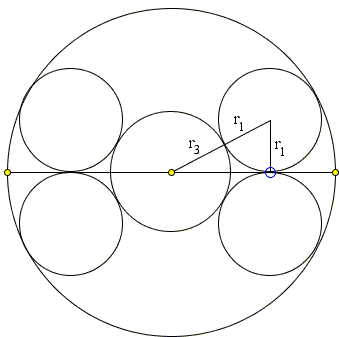
|
| (r3 + r1)² = x² + (r1)². |
implying a quadratic equation
| (r3)² + 2r1r3 - x² = 0. |
The equation has two real roots, a negative one and a positive one, the latter being
| r3 = - r1 + √(r1² + x²) = 0. |
Substituting r1 from (1) gives
| (2) | r3 = x² / r. |
Next in line is r4:

|
for which the Pythagorean theorem provides
| (r - r1 - r4)² + x² = (r1 + r4)². |
One simplification is immediate:
| r² + x² = 2r(r1 + r4), |
Substituting r1 from (1) gives
| r² + x² = r² - x² + 2r·r4, |
from which
| (2) | r4 = x² / r. |
Thus we see that indeed r3 = r4.
When x = r/3, r3 = r4 = r/9. Note that, for this value of x, r1 = 4r/9. Also, circles O1(r1) and O'1(r1) have centers 2x = 2r/3 apart giving the width of the lens shaped intersection as
| 2r1 - 2x = 8r/9 - 2r/3 = 2r/9, |
implying r5 = r/9 = r3 = r4, for x = r/3.
The sangaku ends here, but having a dynamic applet invites an investigation. If the three equal circles grow while the quadruplets become small, the former eventually form 5 regions, into which one may want to inscribed circles:

|
When the five circles are equal, their common radius is r/5; obviously. More can be said, viz., the outer four circles are always equal. Furthermore, their radius is exactly r1 increasing the number of equal circles to 8. The proof is not difficult and is left as an exercise.
References
H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989
Write to:
Charles Babbage Research Center
P.O. Box 272, St. Norbert Postal Station
Winnipeg, MB
Canada R3V 1L6- H. Fukagawa, A. Rothman, Sacred Geometry: Japanese Temple Geometry, Princeton University Press, 2008, p. 101
Sangaku
Resource Limit Is Reached
The website is temporarily unable to service your request as it exceeded resource limit. Please try again later.|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
