A better solution to a difficult sangaku problem

J. Marshall Unger
Department of East Asian Languages & Literatures
The Ohio State University

PROBLEM. In ΔABC, AB = BC. If one chooses D on AB and J on CD such that AJ ⊥ CD and the incircles of ΔACJ, ΔADJ, and ΔBCD all have radius r, then r = AJ/4.

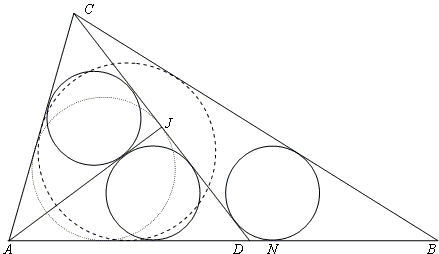
SOLUTION

The trick to solving the problem expeditiously is to clarify what is given and to prove the converse proposition first.

Notice that the only connection between AB = BC and the geometry of ΔACD is that the incircle of ΔABC (dashes) is tangent to AC at its midpoint. The two incircles of ΔACJ and ΔADJ cannot be tangent to the shared side AJ at the same point, as shown, unless J is the point of tangency of the incircle of ΔACD (dots) with side CD [Honsberger, see also Three Incircles in a Triangle]. Hence AC = AD. And the two incircles cannot be congruent unless, in addition, either ∠CAJ = ∠DAJ or AJ ⊥ CD, in which case, ΔACJ = ΔADJ and the other condition follows. Therefore, given a fixed isosceles ABC, if the congruence of all three small incircles implies r = AJ/4, as the problem asserts, then the converse must also be true. Indeed, it is easier to prove.

In the figure above, let a, b, d, and h be the lengths of CD, AD = AC, DN, and AJ, respectively. Let r₁ and r₂ be the radii of the incircles of ΔACD and ΔBCD, respectively. We use two lemmas, which we will prove later:

1.	a - b	= 2d
2.	2 r1r2	= ad

Given h = 4r, square the equation for the inradius of a right triangle: b = h + a/2 - 2r = 2r + a/2 to get b² = 4r² + 2ar + a²/4, and equate this with the Pythagorean result b² = (a/2)² + h² = a²/4 + 16r². This yields a = 6r, which, with h = 4r, implies b = 5r. Hence, by Lemma 1, 2d = r.

Now area( ΔACD) = ha/2 = 12r² = r₁s, where s is the semiperimter of ΔACD or 8r. Thus r₁ = 3r/2 = 3d. Using Lemma 2, we find r₂ = a/6 = r.

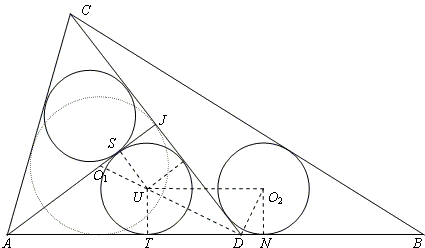
From this, it is clear that solving the original problem comes down to proving, without knowing the value of h, that ΔACJ and ΔADJ are 3:4:5 right triangles.

It's easy to show that ΔDTU is similar to ΔDO₂U. Hence DU is the mean proportional between DT and O₂U = DT + DN. In terms of lengths, we therefore have

	a/2 - r + d	= [r² + (a/2 - r)²] / (a/2 - r)
	(a/2 - r)² + d (a/2 - r)	= r² + (a/2 - r)²
	d (a/2 - r)	= r²
	ad/2 - dr	= r²
	r1r - dr	= r²
	r1 - d	= r.

(Lemma 2 takes the form 2r₁r = ad since we are assuming r₂ = r.) Since JS = r, O₁S = d. Thus JO₁ = r + d = 3d = r₁.

Hence, by Lemma 2, 2rr₁ = 2(2d)(3d) = 12d² = ad, so a = 12d = 6r. Since a - b = 2d (Lemma 1), b = 10d = 5r. And because ADJ is a right triangle, a/2 = 3r and b = 5r imply h = 4r.

The lemmas follow from the general case of any triangle ABC with incircle I. Draw a cevian CD and the incircles O₁ and O₂ of the resulting triangles ACD and BCD. Label the points of tangency of these incircles as shown. Then EH = GK = DN.

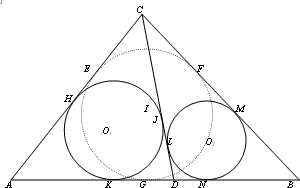
PROOF: By equal tangents, CE = CF (1), and

AE = AG			BF = BG			CM = CL			DJ = DK
AH = AK			BM = BN			CH = CJ			DN = DL.

Subtracting the equations in second row from those in the first, we get

EH = GK (2)

FM = GN (3)

CM - CH = JL (4)

JL = DK - DN (5).

Equating the left and right sides of (4) and (5),

	CM + DN	= DK + CH
	(CF + FM) + DN	= DK + (CE + EH)
	(by 1) FM + DN	= DK + EH
	(by 3) GN + DN	= DK + EH
	(GN - DG) + DN	= (DK - DG) + EH
	2DN	= GK + EH
	(by 2) DN	= GK (6).

Linking equations (2) and (6), EH = GK = DN.

Many more inferences can be drawn from this figure, but we need just two.

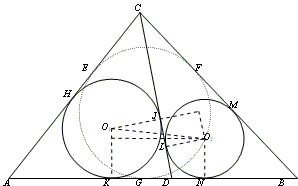
Lemma 1 follows immediately if E and J are the midpoints of AC and CD, respectively. Then CD/2 - AC/2 = EH = DN. In the problem, as explained earlier, J must be the midpoint of CD. Requiring that ABC be isosceles forces E to be the midpoint of AC.

Lemma 2 in the general case is r₁r₂ = DJ·DL. The dashed lines in the figure show that

(r₁ + r₂)² + (DJ - DL)² = (O₁O₂)² = (r₁ - r₂)² + KN²,

but KN = DK + DN = DJ + DL by equal tangents. The rest is just algebra.

In introducing the solution of Kitagawa Moko (1764 -1833), Fukagawa and Rothman remark, "It is somewhat complicated and we hope that readers can find a simpler one." I do not know whether the solution presented above is what Fukagawa and Rothman had in mind, but Kitagawa's solution is certainly complicated. It proves Lemma 1 relying in part on the given that ΔABC is isosceles; finds expressions for r₁, a, and d in terms of r and h; plugs these directly into Lemma 2; produces a third-degree equation in r and h through more painstaking algebra; rejects the roots h = ± r√2 because they are inconsistent with the figure; and so concludes that h = 4r. In addition, Kitagawa's proof gives no hint that the lemmas hold even for scalene ABC, the true significance of requiring that ABC be isosceles, that the converse is true, or that 3:4:5 right triangles play a role.

References

1. H. Fukagawa, A. Rothman, Sacred Mathematics: Japanese Temple Geometry, Princeton University Press, 2008
2. R. Honsberger, Episodes in nineteenth and twentieth-century Euclidean geometry, MAA, 1995

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
   • A Simple Solution to a Difficult Sangaku Problem
   • A Trigonometric Solution to a Difficult Sangaku Problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Chain of Circles on a Chord
21. Circles and Semicircles in Rectangle
22. Circles in a Circular Segment
23. Circles Lined on the Legs of a Right Triangle
24. Equal Incircles Theorem
    • Equal Incircle Theorem, Angela Drei's Proof
25. Equilateral Triangle, Straight Line and Tangent Circles
26. Equilateral Triangles and Incircles in a Square
27. Five Incircles in a Square
28. Four Hinged Squares
29. Four Incircles in Equilateral Triangle
    • Four Incircles in an Equilateral Triangle, a Sangaku
30. Gion Shrine Problem
31. Harmonic Mean Sangaku
32. Heron's Problem
33. In the Wasan Spirit
34. Incenters in Cyclic Quadrilateral
35. Japanese Art and Mathematics
36. Malfatti's Problem
37. Maximal Properties of the Pythagorean Relation
38. Neuberg Sangaku
39. Out of Pentagon Sangaku
40. Peacock Tail Sangaku
41. Pentagon Proportions Sangaku
42. Proportions in Square
43. Pythagoras and Vecten Break Japan's Isolation
44. Radius of a Circle by Paper Folding
45. Review of Sacred Mathematics
46. Sangaku à la V. Thebault
47. Sangaku and The Egyptian Triangle
48. Sangaku in a Square
49. Sangaku Iterations, Is it Wasan?
50. Sangaku with 8 Circles
51. Sangaku with Angle between a Tangent and a Chord
52. Sangaku with Quadratic Optimization
53. Sangaku with Three Mixtilinear Circles
54. Sangaku with Versines
55. Sangakus with a Mixtilinear Circle
56. Sequences of Touching Circles
57. Square and Circle in a Gothic Cupola
58. Steiner's Sangaku
59. Tangent Circles and an Isosceles Triangle
60. The Squinting Eyes Theorem
61. Three Incircles In a Right Triangle
62. Three Squares and Two Ellipses
63. Three Tangent Circles Sangaku
    • An Extension of a Sangaku with Touching Circles
64. Triangles, Squares and Areas from Temple Geometry
65. Two Arbelos, Two Chains
66. Two Circles in an Angle
67. Two Sangaku with Equal Incircles
68. Another Sangaku in Square
69. Sangaku via Peru
70. FJG Capitan's Sangaku

|Up| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny