Two Circles, Ellipse, and Parallel Lines

The problem below has been posted at the CutTheKnotMath facebook page by Cõ Gẫng Lên:

Given circles \(C_{CBEF}\) through \(B, C, E, F\), \(C_{BCGD}\) through \(B,C,D,G\), and ellipse \(E_{BEFCGD}\) through all six points.

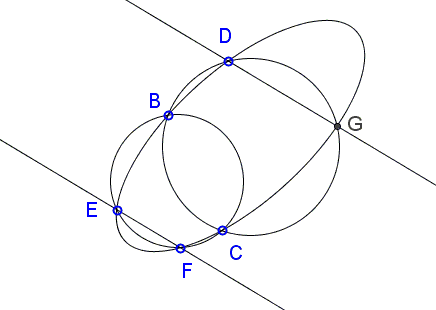
Two circles, ellipse, and two parallel lines

Prove that the lines \(DG\) and \(EF\) are parallel.

Solution

Given circles \(C_{CBEF}\) through \(B, C, E, F\), \(C_{BCGD}\) through \(B,C,D,G\), and ellipse \(E_{BEFCGD}\) through all six points.

Two circles, ellipse, and two parallel lines

Prove that the lines \(DG\) and \(EF\) are parallel.

I shall assume that \(C_{XYZW}\) also denotes the quadratic expression such that \(C_{XYZW} = 0\) is the equation of circle \(C_{XYZW}\) through points \(X,Y,Z,W,\) and similarly for ellipses. In particular, we are given circles \(C_{CBEF}=0,\) \(C_{BCGD}=0,\) and ellipse \(E_{BEFCGD}=0.\) In addition, a line through points \(X,Y\) will be denoted \(L_{XY}\) and defined by the equation \(L_{XY}=0.\)

The pencil of conics through four points \(B, C, E, F\)

\(\lambda C_{CBEF} + \mu E_{BEFCGD} = 0\)

contains a degenerate conic \(L_{BC}\cdot L_{EF} = 0,\) of two (intersecting or parallel) lines \(L_{BC}=0\) and \(L_{EF}=0,\) meaning that, for some fixed \(\lambda_1\) and \(\mu_1,\)

\(L_{BC}\cdot L_{EF} = \lambda_{1} C_{CBEF} + \mu_{1} E_{BEFCGD}.\)

Both \(L_{BC}=0\) and \(L_{EF}=0\) are linear equations.

Similarly, for some fixed \(\lambda_2\) and \(\mu_2,\)

\(L_{BC}\cdot L_{DG} = \lambda_{2} C_{BCGD} + \mu_{2} E_{BEFCGD}.\)

Combining the two equations we obtain

\(L_{BC}\cdot (\mu_{2}L_{EF} - \mu_{1}L_{DG}) = \lambda_{1}\mu_{2}C_{CBEF} - \lambda_{2}\mu_{1}C_{BCGD}.\)

Now, on one hand, equation \(\lambda_{1}\mu_{2}C_{CBEF} - \lambda_{2}\mu_{1}C_{BCGD} = 0\) defines a member of a pencil of circles through points \(B,C.\) This pencil consists of circles (through \(B\) and \(C\)) and their common radical axis \(L_{BC}.\) On the other hand, the left hand side determines the equation \(L_{BC}\cdot (\mu_{2}L_{EF} - \mu_{1}L_{DG})=0\) which defines either two or one line. The two sides may only be equal when both define the same single line which, of necessity, is \(L_{BC}=0,\) implying that \((\mu_{2}L_{EF} - \mu_{1}L_{DG})\) is constant. This is exactly the requirement for \(L_{EF}\) and \(L_{DG}\) to be parallel.

Note: The statement proved above admits an elegant generalization.

Conic Sections > Ellipse

72106479