Angle Bisectors in Ellipse
Let A and B be two points on an ellipse with foci E and F. The tangents to the ellipse at A and B meet in S. Prove that ∠AES = ∠SEB. In words, the point of intersection of two tangents to an ellipse lies on the bisector of the angle formed by joining a focus to the points of tangency.
Conic Sections > Ellipse
- What Is Ellipse?
- Analog device simulation for drawing ellipses
- Angle Bisectors in Ellipse
- Angle Bisectors in Ellipse II
- Between Major and Minor Circles
- Brianchon in Ellipse
- Butterflies in Ellipse
- Concyclic Points of Two Ellipses with Orthogonal Axes
- Conic in Hexagon
- Conjugate Diameters in Ellipse
- Dynamic construction of ellipse and other curves
- Ellipse Between Two Circles
- Ellipse in Arbelos
- Ellipse Touching Sides of Triangle at Midpoints
- Euclidean Construction of Center of Ellipse
- Euclidean Construction of Tangent to Ellipse
- Focal Definition of Ellipse
- Focus and Directrix of Ellipse
- From Foci to a Tangent in Ellipse
- Gergonne in Ellipse
- Pascal in Ellipse
- La Hire's Theorem in Ellipse
- Maximum Perimeter Property of the Incircle
- Optical Property of Ellipse
- Parallel Chords in Ellipse
- Poncelet Porism in Ellipses
- Reflections in Ellipse
- Three Squares and Two Ellipses
- Three Tangents, Three Chords in Ellipse
- Van Schooten's Locus Problem
- Two Circles, Ellipse, and Parallel Lines
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018Alexander Bogomolny
Let A and B be two points on an ellipse with foci E and F. The tangents to the ellipse at A and B meet in S. Prove that ∠AES = ∠SEB. In words, the point of intersection of two tangents to an ellipse lies on the bisector of the angle formed by joining a focus to the points of tangency.
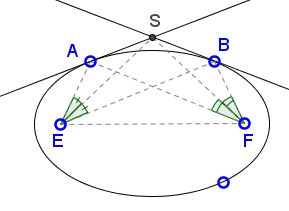
Proof
For a proof, reflect F in the two tangents to obtain points M and N. Because of the reflective property of ellipse, B is collinear with E, N and A with E, M.
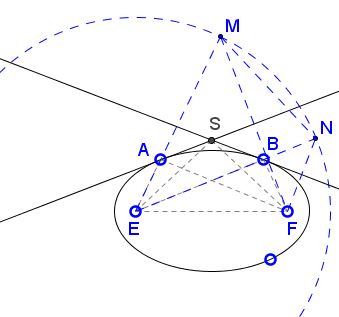
From the definition of ellipse, EA + FA = EB + FB. Since M and N are reflections of F,
| EM | = EA + AM | |
| = EA + FA | ||
| = EB + FB | ||
| = EB + BN | ||
| = EN. |
It follows that ΔMEN is isosceles with
On the other hand, in ΔMFN, tangents AS and BS are the perpendicular bisectors of sides FN and FM. They meet in the circumcenter of ΔMFN, which also lies on the perpendicular bisector of the third side MN. By the construction, S is the point of intersection of the two tangents. Thus S is also the circumcenter of ΔMFN and lies on the perpendicular bisector of MN.
Now return to ΔMEN. Since it is isosceles with base MN, the perpendicular bisector of MN passes through E and plays the role of the bisector of ∠MEN which thus passes through S. But MEN and AEB is one and the same angle, and we are done.
(I thank Hubert Shutrick for his selfless help.)
Conic Sections > Ellipse
- What Is Ellipse?
- Analog device simulation for drawing ellipses
- Angle Bisectors in Ellipse
- Angle Bisectors in Ellipse II
- Between Major and Minor Circles
- Brianchon in Ellipse
- Butterflies in Ellipse
- Concyclic Points of Two Ellipses with Orthogonal Axes
- Conic in Hexagon
- Conjugate Diameters in Ellipse
- Dynamic construction of ellipse and other curves
- Ellipse Between Two Circles
- Ellipse in Arbelos
- Ellipse Touching Sides of Triangle at Midpoints
- Euclidean Construction of Center of Ellipse
- Euclidean Construction of Tangent to Ellipse
- Focal Definition of Ellipse
- Focus and Directrix of Ellipse
- From Foci to a Tangent in Ellipse
- Gergonne in Ellipse
- Pascal in Ellipse
- La Hire's Theorem in Ellipse
- Maximum Perimeter Property of the Incircle
- Optical Property of Ellipse
- Parallel Chords in Ellipse
- Poncelet Porism in Ellipses
- Reflections in Ellipse
- Three Squares and Two Ellipses
- Three Tangents, Three Chords in Ellipse
- Van Schooten's Locus Problem
- Two Circles, Ellipse, and Parallel Lines
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018Alexander Bogomolny
73572005
