Conic in Hexagon
What Might This Be About?
Problem
Let $ABCDEF$ be a hexagon whose diagonals $AD,$ $BE,$ $CF$ concur at a point, say $P.$
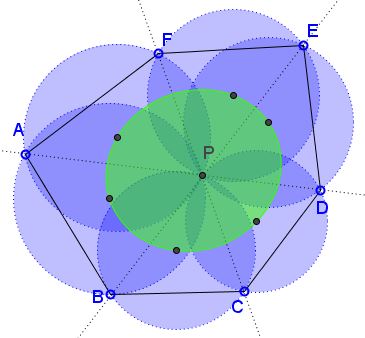
Then the circumcenters of the six triangles formed by the diagonals lie on a conic.
Solution
The result is a direct consequence of the Braikenridge-MacLaurin theorem which is the converse of Pascal's theorem:
If the opposite sides of a hexagon meet at collinear points the vertices of the hexagon lie on a conic.
(This theorem has an interesting story and was published in 1733 in Latin.)
Now, to the problem at hand, the opposite sides of the hexagon in question are parallel because the circumcenters of two adjacent triangles lie on perpendicular bisectors of the common side, which is one of the diagonals of the given hexagon.
It follows that the opposite side lines of the hexagon of circumcenters concur at a point at infinity, such that the three lie on the line at infinity.
Hiroshi Haruki's Conic
A configuration where a hexagon with concurrent diagonals appears is that of Hiroshi Haruki:
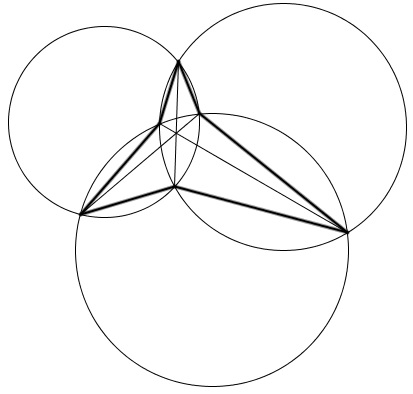
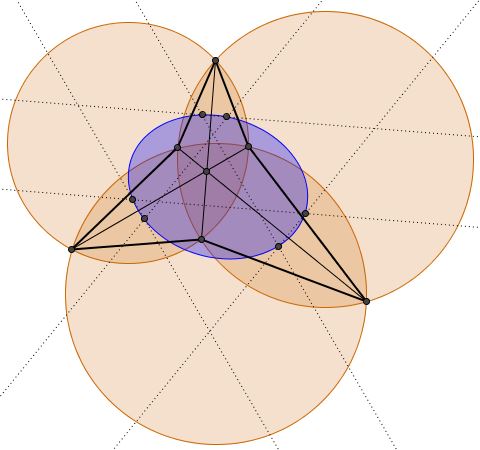
Three circles cros at six points that form a (non-convex) hexagon. The three pairwise radical axes concur at the radical center of the three circles and present the diagonals of the hexagon defined by the six common points. Existence of the associate conic follows:
Acknowledgment
I am grateful to the Italian mathematics teacher Angela Drei for bringing the above to my attention.
Conic Sections > Ellipse
- What Is Ellipse?
- Analog device simulation for drawing ellipses
- Angle Bisectors in Ellipse
- Angle Bisectors in Ellipse II
- Between Major and Minor Circles
- Brianchon in Ellipse
- Butterflies in Ellipse
- Concyclic Points of Two Ellipses with Orthogonal Axes
- Conic in Hexagon
- Conjugate Diameters in Ellipse
- Dynamic construction of ellipse and other curves
- Ellipse Between Two Circles
- Ellipse in Arbelos
- Ellipse Touching Sides of Triangle at Midpoints
- Euclidean Construction of Center of Ellipse
- Euclidean Construction of Tangent to Ellipse
- Focal Definition of Ellipse
- Focus and Directrix of Ellipse
- From Foci to a Tangent in Ellipse
- Gergonne in Ellipse
- Pascal in Ellipse
- La Hire's Theorem in Ellipse
- Maximum Perimeter Property of the Incircle
- Optical Property of Ellipse
- Parallel Chords in Ellipse
- Poncelet Porism in Ellipses
- Reflections in Ellipse
- Three Squares and Two Ellipses
- Three Tangents, Three Chords in Ellipse
- Van Schooten's Locus Problem
- Two Circles, Ellipse, and Parallel Lines
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575467
