A Simple Solution to a Difficult Sangaku Problem

Nikolaos Dergiades
Thessaloniki Greece
May 15, 2017

Chapter 6, problem 3, sangaku from Fukagawa & Rothman

Solution

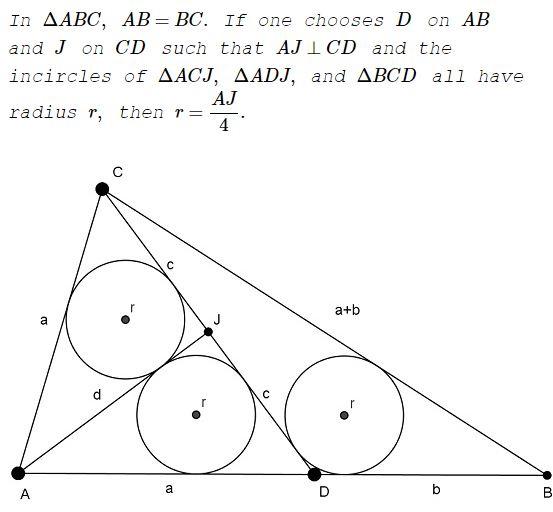
Since the incircles of triangles $AJC,\,$ $AJD\,$ are symmetric relative to $AJ,\,$ the same holds for $AC,\,$ $AD\,$ and hence $AC=AD=a,\,$ $CJ=JD=c.\,$

If $AJ=d,\,$ $DB=b,\,$ then $BC=a+b.$

From $\Delta CDB,\,$ $\displaystyle r=\frac{2[CDB]}{CD+DB+BA}=\frac{[CDB]}{\displaystyle \frac{a}{2}+b+c}.$

From $\Delta CAJ,\,$ $\displaystyle r=\frac{2[CAJ]}{a+c+d}=\frac{[CAD]}{a+c+d}.$

Hence, $\displaystyle \frac{b}{a}=\frac{[CDB]}{[CAD]}=\frac{\displaystyle \frac{a}{2}+b+c}{\displaystyle a+c+d}=\frac{\displaystyle \frac{a}{2}+c}{\displaystyle c+d},$

from which

(1)

$\displaystyle b=\frac{a(a+2c)}{2(c+d)}.$

Stewart's theorem gives,

$CA^2\cdot DB+CB^2\cdot AD=CD^2\cdot AB+AD\cdot DB\cdot AB,$

i.e., $a^2b+(a+b)^2a=4c^2(a+b)+ab(a+b),\,$ from which

(2)

$\displaystyle b=\frac{a(4c^2-a^2)}{2(a^2-2c^2)}.$

From (1) and (2) we conclude that $a^2-2c^2\ne 0\,$ and $\displaystyle c+d=\frac{a^2-2c^2}{2c-a}.$

In $\Delta CAJ,\,$ the Pythagorean theorem gives $a^2-c^2=d^2,\,$ such that $a^2-2c^2=(d+c)(d-c)\,$ and

$\displaystyle a^2-2c^2=\frac{a^2-2c^2}{2c-a}\cdot\frac{a^2+2ac-6c^2}{2c-a},$

implying $3a=5c,\,$ or $a=5x,\,$ $c=3x,\,$ $d=4x\,$ and, since $a=(c-r)+(d-r),\,$ we get $\displaystyle r=x=\frac{d}{4}=\frac{AJ}{4}.$

Sangaku

71940024

A Simple Solution to a Difficult Sangaku Problem

Nikolaos Dergiades Thessaloniki Greece May 15, 2017

Solution

Sangaku

Nikolaos Dergiades
Thessaloniki Greece
May 15, 2017