3-4-5 Triangle by a Kid

It is often said that the practice of hanging sangaku was so common that even women and children took part in that activity. While there is a reasonable doubt as to the popularity of sangaku, there is no question that some were hung by very young children. The one below was proposed by Sato Naosue, age thirteen, and hung in 1847 in the Akahagi Kannon temple in Ichinoseki city.

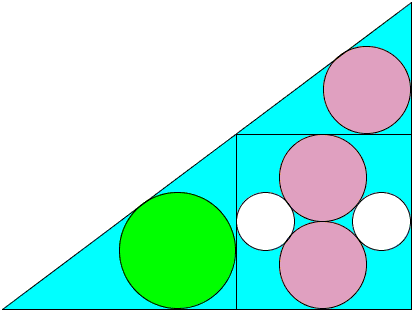
Two pink circles of radius $r$ and two white circles of radius $t$ are inscribed in a square, as shown. The square itself is inscribed in a large triangle and, as illustrated, two circles of radii $r$ and $R$ are inscribed in the small triangles outside the square. Show that $R = 2t$.

Solution

References

H. Fukagawa, A. Rothman, Sacred Mathematics: Japanese Temple Geometry, Princeton University Press, 2008, pp. 104-105

Sangaku

Obviously, the side of the square is of length $4r.$ One application of the Pythagorean theorem (in the dashed triangle) shows that $r = 3t/2.$ Use the Pythagorean theorem again in the small upper triangle:

Let $a$ be the small length of that triangle and $c$ its hypotenuse. On the other hand, the area $S$ of the small triangle can be computed in two ways:

$2S=r(a+c+4r)=4r\cdot a,$

such that $a+c+4r=4a;$ from which $c=3a-4r.$ Substitute that into the Pythagorean identity - $a^2+(4r)^2=c^2$ - to get the equation

$a^2+16r^2=(3a-4r)^2,$

solving which gives $a=3r.$

It may come as a surprise that the triangle turns out to be the famous 3-4-5 or Egyptian triangle with the short side equal to $3r.$ From the similarity of the three triangles, all of them have the proportions 3-4-5 which leads to $4r = 3R.$ And finally, $R = 4r/3 = 2t.$

72533674