Maximum Perimeter Property of the Incircle

Given point P, points A, B, C are at fixed distances AP, BP, and CP from P. Among all triangles ABC, the one for which P is the incenter, has the maximum perimeter.

The claim amounts to the assertion that, for the optimal triangle ABC, P lies on the bisectors of all three angles of the triangle. The applet below illustrates the fact that no other triangle may possibly has the maximum perimeter.

In the applet, point P always moves freely. The effect of dragging points A, B, C depends on which of the two boxes -- "Adjust circles" or "Move points" -- is checked. When the latter is checked, points A, B, C move on circles centered at P. Otherwise, they move freely.

When one of the points A, B, or C is being dragged, the applet displays a family of confocal ellipses with foci at the other two points. Assume A is being dragged. In this case, BC is constant so that the change in the magnitude of the perimeter AB + BC + CA is reflected in the change of the sum f(A) = AB + CA. This sum is constant on the ellipses with the foci at B and C. Let A move on a circle C(P), with center P. Function f(P) cannot have a (local) maximum wherever C(P) intersects the ellipses, but only when it is tangent to one of them. In principle, there are two such ellipses. At the point of tangency with one of them f(p) attains a global maximum. 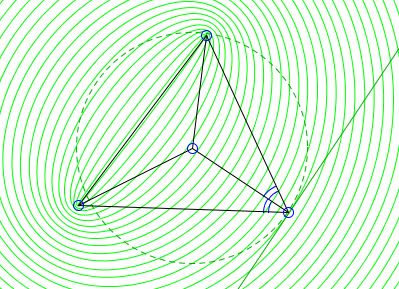At the points of tangency, C(P) shares the tangent with the corresponding ellipse. But ellipse is known to possess the mirror property: the lines joining the foci to a point on the ellipse form equal angles with the tangent, meaning, in particular, that the perpendicular to the tangent at that point serves as the bisector of angle BAC. But the perpendicular to a tangent on a point of a circle is a radius of the circle, so that, for such point A where C(P) is tangent to on of the ellipses, AP is the bisector of angle BAC.

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

The function f(A, B, C) = AB + BC + CA is a continuous function of its arguments. The Cartesian product of three circles with radii AP, BP, CP centered at P is a compact set so that the function does attain its maximum. For the corresponding triangle ABC, AP, BP, and CP must be angle bisectors of angles BAC, ABC, ACB, respectively, implying that P is the incenter of that triangle.

Ellipse

Conic Sections > Ellipse

• What Is Ellipse?
  
• Analog device simulation for drawing ellipses
• Angle Bisectors in Ellipse
• Angle Bisectors in Ellipse II
• Between Major and Minor Circles
• Brianchon in Ellipse
• Butterflies in Ellipse
• Concyclic Points of Two Ellipses with Orthogonal Axes
• Conic in Hexagon
• Conjugate Diameters in Ellipse
• Dynamic construction of ellipse and other curves
• Ellipse Between Two Circles
• Ellipse in Arbelos
• Ellipse Touching Sides of Triangle at Midpoints
• Euclidean Construction of Center of Ellipse
• Euclidean Construction of Tangent to Ellipse
• Focal Definition of Ellipse
• Focus and Directrix of Ellipse
• From Foci to a Tangent in Ellipse
• Gergonne in Ellipse
• Pascal in Ellipse
• La Hire's Theorem in Ellipse
• Maximum Perimeter Property of the Incircle
• Optical Property of Ellipse
• Parallel Chords in Ellipse
• Poncelet Porism in Ellipses
• Reflections in Ellipse
• Three Squares and Two Ellipses
• Three Tangents, Three Chords in Ellipse
• Van Schooten's Locus Problem
• Two Circles, Ellipse, and Parallel Lines

|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|

Copyright © 1996-2015 Alexander Bogomolny