Triangles, Squares and Areas from Temple Geometry
The problem presented by the applet below has been plucked from a collection of Temple Geometry Problems. Down below, I'll give three solutions, the first being drawn from another collection.
Problem
Five squares are arranged as in the applet. Show that the area of triangle KMN equals the area of the square BEKH.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Five squares are arranged as in the applet. Show that the area of triangle KMN equals the area of the square BEKH.
First of all note that angles ABE and CBJ being complementary, right triangle ABE and BCH are congruent. Therefore, if we denote AB as a and BC as b,
CY = CH = AB = a, and
XA = AE = BC = b.
Solution 1
The construction needed for the first solution is hinted to in the applet.
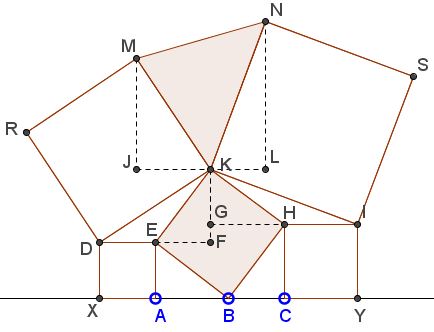
Observe that triangles EFK and GHK are congruent to ABE and BCH. Thus, also
EF = GK = a, and
FK = GH = b.
This makes DF = 2a and GI = 2b. Now, triangles DFK and JKM are congruent, as are triangles GIK and KLN, so that
JK = FK = b,
JM = DF = 2a,
KL = GK = a,
LN = GI = 2b.
We see that
| Area(KMN) | = Area(JMNL) - Area(JKM) - Area(KLN) |
| = (a + b)(2a + 2b)/2 - 2a·b/2 - a·2b/2 | |
| = (a + b)² - 2ab | |
| = a² + b² | |
| = Area(BEKH). |
Solution 2
The only additional construction needed is line DI, which is not actually shown. The diagram presents several Vecten configurations, from which we conclude that triangles ABE, DEK, BCH, KHI have equal areas, as are triangles KMN and DIK.
| Area(KMN) | = Area(DIK) |
| = Area(DXYIK) - Area(DXYI) | |
| = (a² + b² + 4ab/2 + a² + b²) - (2a + 2b)(a + b)/2 | |
| = 2a² + 2b² + 2ab - a² - 2ab - b² | |
| = a² + b² | |
| = Area(BEKH). |
Solution 3
Compared to the first solution, the second one draws very little on algebra. The third solution suggested by Nathan Bowler continues the progression: on the surface it does not use any algebra at all. I placed it on a separate page.
References
- H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989, #4.2.4
- J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996, #50
Sangaku
- Sangaku: Reflections on the Phenomenon
- Critique of My View and a Response
- 1 + 27 = 12 + 16 Sangaku
- 3-4-5 Triangle by a Kid
- 7 = 2 + 5 Sangaku
- A 49th Degree Challenge
- A Geometric Mean Sangaku
- A Hard but Important Sangaku
- A Restored Sangaku Problem
- A Sangaku: Two Unrelated Circles
- A Sangaku by a Teen
- A Sangaku Follow-Up on an Archimedes' Lemma
- A Sangaku with an Egyptian Attachment
- A Sangaku with Many Circles and Some
- A Sushi Morsel
- An Old Japanese Theorem
- Archimedes Twins in the Edo Period
- Arithmetic Mean Sangaku
- Bottema Shatters Japan's Seclusion
- Chain of Circles on a Chord
- Circles and Semicircles in Rectangle
- Circles in a Circular Segment
- Circles Lined on the Legs of a Right Triangle
- Equal Incircles Theorem
- Equilateral Triangle, Straight Line and Tangent Circles
- Equilateral Triangles and Incircles in a Square
- Five Incircles in a Square
- Four Hinged Squares
- Four Incircles in Equilateral Triangle
- Gion Shrine Problem
- Harmonic Mean Sangaku
- Heron's Problem
- In the Wasan Spirit
- Incenters in Cyclic Quadrilateral
- Japanese Art and Mathematics
- Malfatti's Problem
- Maximal Properties of the Pythagorean Relation
- Neuberg Sangaku
- Out of Pentagon Sangaku
- Peacock Tail Sangaku
- Pentagon Proportions Sangaku
- Proportions in Square
- Pythagoras and Vecten Break Japan's Isolation
- Radius of a Circle by Paper Folding
- Review of Sacred Mathematics
- Sangaku à la V. Thebault
- Sangaku and The Egyptian Triangle
- Sangaku in a Square
- Sangaku Iterations, Is it Wasan?
- Sangaku with 8 Circles
- Sangaku with Angle between a Tangent and a Chord
- Sangaku with Quadratic Optimization
- Sangaku with Three Mixtilinear Circles
- Sangaku with Versines
- Sangakus with a Mixtilinear Circle
- Sequences of Touching Circles
- Square and Circle in a Gothic Cupola
- Steiner's Sangaku
- Tangent Circles and an Isosceles Triangle
- The Squinting Eyes Theorem
- Three Incircles In a Right Triangle
- Three Squares and Two Ellipses
- Three Tangent Circles Sangaku
- Triangles, Squares and Areas from Temple Geometry
- Two Arbelos, Two Chains
- Two Circles in an Angle
- Two Sangaku with Equal Incircles
- Another Sangaku in Square
- Sangaku via Peru
- FJG Capitan's Sangaku
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73356836
