Many sangaku problems include circle and ellipses, but quite a few do not. An elegant one [Fakagawa & Pedoe, p. 49] with a rather computational solution is presented below.

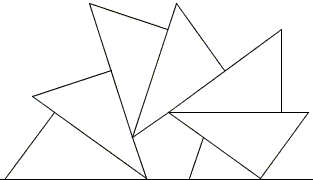
6 congruent right triangles fan out along the sides of a regular pentagon of side a. Find the length of the hypotenuse t of these triangles in terms of a.

This sangaku appears on a extant tablet in the Miyagai prefecture. Unless there is a misprint, [Fakagawa & Pedoe, p. 134] dates the tablet from 1912.

Solution

References

1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

   Write to:

   Charles Babbage Research Center
   P.O. Box 272, St. Norbert Postal Station
   Winnipeg, MB
   Canada R3V 1L6

Copyright © 1996-2009 Alexander Bogomolny

We can imagine a couple of right triangles with sides computable from the Pythagorean theorem that combine into the altitude of one of the congruent triangles:

Given that the internal angle of a regular pentagon is 108°, one of the triangles has angles 36°- 54°- 90°, the other 18°- 72°- 90°.

The altitude in question equals

h = a·(sin(36°) + sin(72°)).

The fan forming triangles are also of the 36°- 54°- 90° variety since two of their smallest angles supplement 108°. In such a triangle the hypotenuse t is expressable in terms of the altitude:

t = h·(tan(36°) + tan(54°)).

Combining the two we get

t = a·(tan(36°) + tan(54°))·(sin(36°) + sin(72°)).

The solution t = a·(1 + √5) given by [Fakagawa & Pedoe] tells us that the expression for t, if correct, is amenable to a simplification effort.

Let's denote c = cos(36°) and s = sin(36°). By the Pythagorean theorem c² + s² = 1. In addition, tan(36°) = s/c, and tan(54°) = cot(36°) = c/s, since 36° and 54° are supplementary angles. Also, sin(72°) = 2sc. We see that t can be written as

This must be transformed further taking into account that c = (1 + √5)/4. To continue,

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Circles and Semicircles in Rectangle
21. Circles in a Circular Segment
22. Circles Lined on the Legs of a Right Triangle
23. Equal Incircles Theorem
24. Equilateral Triangle, Straight Line and Tangent Circles
25. Equilateral Triangles and Incircles in a Square
26. Five Incircles in a Square
27. Four Hinged Squares
28. Four Incircles in Equilateral Triangle
29. Gion Shrine Problem
30. Harmonic Mean Sangaku
31. Heron's Problem
32. In the Wasan Spirit
33. Incenters in Cyclic Quadrilateral
34. Japanese Art and Mathematics
35. Malfatti's Problem
36. Maximal Properties of the Pythagorean Relation
37. Neuberg Sangaku
38. Out of Pentagon Sangaku
39. Peacock Tail Sangaku
40. Pentagon Proportions Sangaku
41. Pythagoras and Vecten Break Japan's Isolation
42. Radius of a Circle by Paper Folding
43. Review of Sacred Mathematics
44. Sangaku à la V. Thebault
45. Sangaku and The Egyptian Triangle
46. Sangaku in a Square
47. Sangaku Iterations, Is it Wasan?
48. Sangaku with 8 Circles
49. Sangaku with Three Mixtilinear Circles
50. Sangaku with Versines
51. Sangakus with a Mixtilinear Circle
52. Sequences of Touching Circles
53. Square and Circle in a Gothic Cupola
54. Tangent Circles and an Isosceles Triangle
55. The Squinting Eyes Theorem
56. Steiner's Sangaku
57. Three Incircles In a Right Triangle
58. Three Squares and Two Ellipses
59. Three Tangent Circles Sangaku
60. Triangles, Squares and Areas from Temple Geometry
61. Two Arbelos, Two Chains
62. Two Circles in an Angle
63. Two Sangaku with Equal Incircles

Copyright © 1996-2009 Alexander Bogomolny