Radius of a Circle by Paper Folding

Finding the radius of a circle without special tools is not a trivial matter, unless, of course, you are aware of a Sangaku problem. Sangaku, a mathematical tablet in Japanese, was an art form that flourished during the period of self-imposed seclusion that lasted about 200 years. No one exactly knows how the tradition came about. The purpose might have been to challenge the contemporaries or please the gods. However, the one presented by the applet below seems to have a very specific and practical application: determining the radius of a circle with paper folding - an ancient Japanese art form.

Created with GeoGebra

Solution

(The are more problems from Temple geometry.)

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

One solution - mostly algebraic - depends on the derivation from the paper folding algorithm for subdivision of a segment into equal parts. Thus assume that we are given a square (ABCD) piece of paper of side 1 and a circle fitted snugly into the C corner. Let X be a point on BC and k = BX/BC (= BX). We then have:

CP = 2k/(1 + k),

and from the Pythagorean proposition applied to triangle XCP,

XP = (1 + k²) / (1 + k).

Further, since NP = 1 - XP,

(1)	NP = k(1 - k) / (1 + k).

(Thanks are due to a very rude Frenchman who pointed out an error in the original derivation.) Now recollect that in a right triangle with legs a and b and hypotenuse c, the inradius equals

(2)	r = (a + b - c)/2

which, when applied to triangle XCP gives exactly (1).

It follows, that if the corner A is folded into a point X such that the edge XP of the paper touches the given circle, the protruding piece NP will give exactly the radius of the circle.

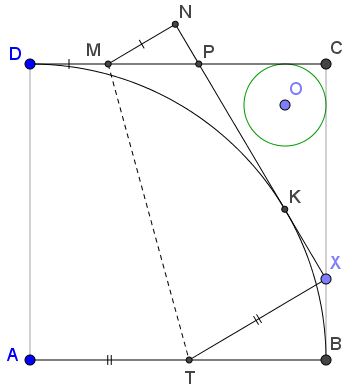
A geometric solution has been suggested by Nathan Bowler.

Observe that circle of radius 1 centered at X is tangent to AD. By symmetry, the unit circle with center at A is tangent to XP. Since it is also tangent to BC and CD, it is the excircle of DXCP opposite vertex C. Let K be the point of tangency of the circle and XP. Then PK = PD (two tangents from P) and XK = XB (two tangents from X. It follows that the perimeter DXCP equals

CP + XP + XC = CD + BC = 2.

Let s = 1 be the semiperimeter of the triangle. The formula (2) for the inradius can be rewritten as

(2')	r = s - c = s - XP = 1 - XP.

However XN = AD = 1, so that 1 - XP = XN - XP = NP.

The tablet on which this problem was depicted in 1893 in the Fukusima prefecture still survives, and is described in 1967 publication by Akira Hirayama and Hachio Norii, with a reference to an earlier manuscript with a probable title of Reikan Sanpo Syokia (Correction of Some Problems) by Teisuke Hagiwara. For the sake of comparison, I include that proof below.

The triangle NMP is a right triangle, and NM = DM. Let r₀ be the inradius of triangle NMP, and r the inradius of triangle PCX. Then PX = NX - NP, CP = CD - (NM + MP), 2r₀ = NM + NP - MP. From r : CP = r₀ : NP,

r·NP = r₀·CP = r₀·CD - r₀·(NM + MP),

and from r : PX = r₀ : MP,

r·MP = r₀·PX = r₀·(NX - NP).

Hence

r·(MP - NP)	= r0·(NM + MP - NP)
	= ½(NM + NP - MP)(NM - NP + MP)
	= ½(NM² - NP² + 2·NP·MP - MP²)
	= ½(2·NP·MP - 2·NP²)
	= NP·(MP - NP),

and r = NP.

Problem

It is not at all obvious that the above construction is based on the axioms of paper folding. Can this be done, or is it a paper folding neusis construction?

The original sangaku presents an entertaining geometric problem with paper folding overtones. It should not, however, be seen as a definitive paper folding way of determining the radius of circular objects. As Sam Zbarsky, a young relative of mine (now 10) whom we met on another occasion, notes there is a much simpler way of finding the radius if need be by paper folding. The approach is illustrated by the following diagram:

References

1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

   Write to:

   Charles Babbage Research Center
   P.O. Box 272, St. Norbert Postal Station
   Winnipeg, MB
   Canada R3V 1L6

2. R. Honsberger, More Mathematical Morsels, MAA, 1991, pp. 8-12

Paper Folding Geometry

• An Interesting Example of Angle Trisection by Paperfolding
• Angle Trisection by Paper Folding
• Angles in Triangle Add to 180^o
• Broken Chord Theorem by Paper Folding
• Dividing a Segment into Equal Parts by Paper Folding
• Egyptian Triangle By Paper Folding
• Egyptian Triangle By Paper Folding II
• Egyptian Triangle By Paper Folding III
• My Logo
• Paper Folding And Cutting Sangaku
• Parabola by Paper Folding
• Radius of a Circle by Paper Folding
• Regular Pentagon Inscribed in Circle by Paper Folding
• Trigonometry by Paper Folding
• Folding Square in a Line through the Center
• Tangent of 22.5^o - Proof Without Words
• Regular Octagon by Paper Folding
• The Shortest Crease
• Fold Square into Equilateral Triangle
• Circle Center by Paperfolding
• Folding and Cutting a Square

Related material Read more...
	Right Pentagonal Prism
	Square Pyramid
	Right Triangular Prism
	Twisted Triangular Prism
	Tetrahedron: an Interactive Model
	Octahedron: an Interactive Model
	Cube: an Interactive Model
	Icosahedron: an Interactive Model
	Dodecahedron: an Interactive Model
	Three Pyramids are Better Than Two
	Cube In Octahedron
	Octahedron In Cube
	Octahedron In Tetrahedron
	Tetrahedron In Cube
	Icosahedron In Cube
	Great Stellated Dodecahedron
	Lennes' Polyhedron
	Triangulated Dinosaur
	Volumes of Two Pyramids
	Császár Polyhedron 1
	Császár Polyhedron 4
	Szilassi Polyhedron
	Dissection of a Square Pyramid

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny