Equilateral Triangles and Incircles in a Square

Here is an elegant sangaku that requires both geometric and algebraic skills and some perseverance:


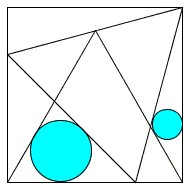
Two equilateral triangles are inscribed into a square as shown in the diagram. Their side lines cut the square into a quadrilateral and a few triangles. Find a relationship between the radii of the two incircles shown in the diagram.

Solution

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny


Two equilateral triangles are inscribed into a square as shown in the diagram. Their side lines cut the square into a quadrilateral and a few triangles. Find a relationship between the radii of the two incircles shown in the diagram.

At first sight, the problem may appear surprising: do indeed equilateral triangles form such a configuration in a square? As a matter of fact they do so even in a more general setting. As a result, we may find all the angles in the diagram as shown below (in degrees):

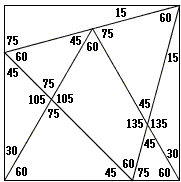
For the sake of convenience we label relevant points:

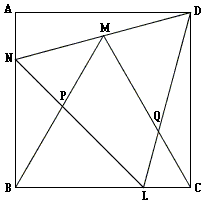
and add four more: the projections of M, P, and Q on the sides of the square.

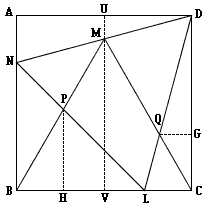
Assume the side of the square equals 2: AB = BC = CD = AD = BM = CM = 2. Then in equilateral ΔBCM, the altitude MV = √3, the remainder MU = 2 - √3. From here (in ΔDUM) we can determine the values of trigonometric functions at 15° which will be useful later on. First

tan 15° = 2 - √3.

By the Pythagorean theorem,

MD2= UD2 + MU2
 = 1 + (2 - √3)2
 = 1 + 4 - 4√3 + 3
 = 8 - 4√3
 = 2·(4 - 2√3)
 = 2·(1 - √3)2

so that finally

MD = √2·(√3 - 1) = √6 - √2.

Thus we can find sin 15° and cos 15°:

sin 15°= UM / DM
 = (2 - √3) / (√6 - √2)
 = (√6 - √2) / 4 and, similarly,
cos 15°= (√6 + √2) / 4.

Now continue. ΔDAN is a doubled replica of ΔDUM so that AN = 2(2 - √3). Therefore,

BN = BL = 2(√3 - 1).

After these preliminaries we are in a position to tackle triangles BLP and CDQ. Because of a proliferation of radicals it is a convenience to begin with similar triangles B'L'P' and C'D'Q' in which B'H' = 1 and G'Q' = 1. The other lengths come out as follows:

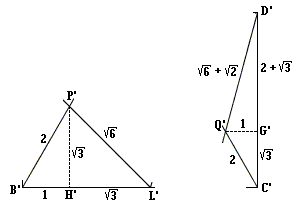
We apply the same standard formula as in another sangaku:

rp = 2S = ah,

where r, p, S, a, h are respectively the inradius, perimeter, area, a side and the altitude to the side in a triangle. In ΔB'L'P', the inradius is found to be

r' = √3·(1 + √3) / (3 + √3 + √6) = (1 + √3) / (1 + √2 + √3).

The inradius r1 of ΔBLP relates to r' as the ratio of the sides, e.g. BL/B'L' which is

BL/B'L' = 2(√3 - 1) / (1 + √3) = 2(2 - √3),

from which

(1) r1 = 2(√3 - 1) / (1 + √2 + √3).

Similarly, the inradius r2 of ΔCDQ can be found to be

(2) r2 = 2 / (4 + 2√3 + √6 + √2).

With an additional effort, we conclude that (1) and (2) imply

r1 = 2r2.

And this is the relationship we were supposed to surmise from the diagram.

It goes without saying that any use of calculators (direct or implicit via dynamic geometry software) to solve this problem is rather inappropriate as the calculations would conceal rather than help discover patterns between various elements of the diagram. Check a remark on another page and the last chapter of an exceptional book by D. Niederman and D. Boyum.

An anonymous visitor to the site has observed that the original diagram contains great many triangles, each with the incircle. The visitor drew attention to a pair of equal ones and conjectured that there are more such pairs of twin circles.

The visitor has surmised that line PQ is perpendicular to LQ which shows that in the right ΔLPQ, angle at P is 30°, so that the hypotenuse LP is twice as long as the leg opposite angle P:

LP = 2·LQ.

Additionally triangles CQL and BLP are similar:

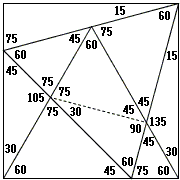
In the similar triangles CQL and BLP a pair of corresponding sides (LP : LQ) is in the ratio 2 : 1 implying the same ratio for other linear elements. In particular, the inradii of the two triangles are in the ratio 2 : 1.

It follows that the incircles of triangles CQL and CDQ are equal. One then wonders whether another sangaku would not be more natural.

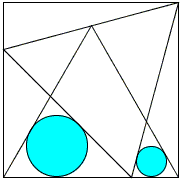
However, simple comparison of the computed radii of various circles shows that besides the pair ADN and CDL of equal triangles, the diagram contains no twin circles in addition to the pair CQL and CDQ. Following is the collection of the radii of all the circles that appear in the double diagram above:

30.897424740513205
15.44871237025661
21.847778555217914
20.843374709207808
21.020708950586016
15.448712370256642
29.844620522684522
26.757954736802247
34.75479670426888
20.358888551841012
37.52222553867126
20.358888551840977
25.527816277595395
13.850936587751294
28.47257935337593

Most of the differences between the numbers in the list are sufficiently large to be explained by the accuracy (or the lack thereof) of calculations. Thus here is an example where the mathematical truth, albeit negative, can be established with the help of calculators.

References

  1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

    Write to:

    Charles Babbage Research Center
    P.O. Box 272, St. Norbert Postal Station
    Winnipeg, MB
    Canada R3V 1L6

  2. D. Niederman and D. Boyum, What The Numbers Say, Broadway Books, 2003

Sangaku

  1. Sangaku: Reflections on the Phenomenon
  2. Critique of My View and a Response
  3. 1 + 27 = 12 + 16 Sangaku
  4. 3-4-5 Triangle by a Kid
  5. 7 = 2 + 5 Sangaku
  6. A 49th Degree Challenge
  7. A Geometric Mean Sangaku
  8. A Hard but Important Sangaku
  9. A Restored Sangaku Problem
  10. A Sangaku: Two Unrelated Circles
  11. A Sangaku by a Teen
  12. A Sangaku Follow-Up on an Archimedes' Lemma
  13. A Sangaku with an Egyptian Attachment
  14. A Sangaku with Many Circles and Some
  15. A Sushi Morsel
  16. An Old Japanese Theorem
  17. Archimedes Twins in the Edo Period
  18. Arithmetic Mean Sangaku
  19. Bottema Shatters Japan's Seclusion
  20. Chain of Circles on a Chord
  21. Circles and Semicircles in Rectangle
  22. Circles in a Circular Segment
  23. Circles Lined on the Legs of a Right Triangle
  24. Equal Incircles Theorem
  25. Equilateral Triangle, Straight Line and Tangent Circles
  26. Equilateral Triangles and Incircles in a Square
  27. Five Incircles in a Square
  28. Four Hinged Squares
  29. Four Incircles in Equilateral Triangle
  30. Gion Shrine Problem
  31. Harmonic Mean Sangaku
  32. Heron's Problem
  33. In the Wasan Spirit
  34. Incenters in Cyclic Quadrilateral
  35. Japanese Art and Mathematics
  36. Malfatti's Problem
  37. Maximal Properties of the Pythagorean Relation
  38. Neuberg Sangaku
  39. Out of Pentagon Sangaku
  40. Peacock Tail Sangaku
  41. Pentagon Proportions Sangaku
  42. Proportions in Square
  43. Pythagoras and Vecten Break Japan's Isolation
  44. Radius of a Circle by Paper Folding
  45. Review of Sacred Mathematics
  46. Sangaku à la V. Thebault
  47. Sangaku and The Egyptian Triangle
  48. Sangaku in a Square
  49. Sangaku Iterations, Is it Wasan?
  50. Sangaku with 8 Circles
  51. Sangaku with Angle between a Tangent and a Chord
  52. Sangaku with Quadratic Optimization
  53. Sangaku with Three Mixtilinear Circles
  54. Sangaku with Versines
  55. Sangakus with a Mixtilinear Circle
  56. Sequences of Touching Circles
  57. Square and Circle in a Gothic Cupola
  58. Steiner's Sangaku
  59. Tangent Circles and an Isosceles Triangle
  60. The Squinting Eyes Theorem
  61. Three Incircles In a Right Triangle
  62. Three Squares and Two Ellipses
  63. Three Tangent Circles Sangaku
  64. Triangles, Squares and Areas from Temple Geometry
  65. Two Arbelos, Two Chains
  66. Two Circles in an Angle
  67. Two Sangaku with Equal Incircles
  68. Another Sangaku in Square
  69. Sangaku via Peru
  70. FJG Capitan's Sangaku

Related material
Read more...

  • Equilateral Triangles on Sides of a Quadrilateral
  • Euler Line Cuts Off Equilateral Triangle
  • Four Incircles in Equilateral Triangle
  • Problem in Equilateral Triangle
  • Problem in Equilateral Triangle II
  • Sum of Squares in Equilateral Triangle
  • Triangle Classification
  • Isoperimetric Property of Equilateral Triangles
  • Maximum Area Property of Equilateral Triangles
  • Angle Trisectors on Circumcircle
  • Equilateral Triangles On Sides of a Parallelogram
  • Pompeiu's Theorem
  • Circle of Apollonius in Equilateral Triangle

    • |Contact| |Front page| |Contents| |Geometry| |Up|

    Copyright © 1996-2018 Alexander Bogomolny

    72393554