Sum of Squares in Equilateral Triangle
Here's problem #86 from a charming collection by C. W. Trigg, the long term editor of the Problems sections at the Mathematics Magazine.
| |
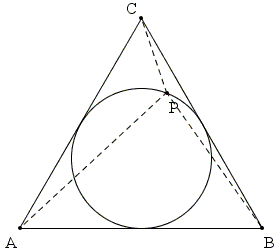
If ABC is an equilateral triangle, and P is any point on the incircle of ΔABC, prove that
| | AP² + BP² + CP² is constant. |
|
Solution
Reference
- C. W. Trigg, Mathematical Quickies, Dover, 1985
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
| |
If ABC is an equilateral triangle, and P is any point on the incircle of ΔABC, prove that
| | AP² + BP² + CP² is constant. |
|
Solution
Trigg credits Leo Moser with the following solution.
Think of the whole diagram as being drawn in three dimensions, so that A = (1, 0, 0), B = (0, 1, 0), C = (0, 0, 1), making the three points lie in the plane x + y + z = α (in fact, α = 1, in this case, but this is convenient to think of it as a generic constant for the sake of a lurking generalization.) The incircle of ΔABC is the intersection of that plane with the sphere x² + y² + z² = β, another constant.
For P on the incircle,
| | AP² + BP² + CP² | = (1 - x)² + y² + z² +
x² + (1 - y)² + z +
x² + y² + (1 - z)² |
| | | = 3(x² + y² + z²) - 2(x + y + z) + 3 |
| | | = 3β - 2α + 3 |
| | | = constant. |
Observe that the proof goes through for any circle concentric to the incircle. A more general result claims that the sum of squares of the distances from a point to the vertices of a triangle - not necessarily equilateral - is constant for every circle with center at the centroid of the triangle.
2D Problems That Benefit from a 3D Outlook
- Four Travellers, Solution
- Desargues' Theorem
- Soddy Circles and Eppstein's Points
- Symmetries in a Triangle
- Three Circles and Common Chords
- Three Circles and Common Tangents
- Three Equal Circles
- Menelaus from 3D
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Sum of Squares in Equilateral Triangle
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
|
