Triangle Classification
The basic elements of any triangle are its sides and angles. Triangles are classified depending on relative sizes of their elements.
As regard their sides, triangles may be
- Scalene (all sides are different)
- Isosceles (two sides are equal)
- Equilateral (all three sides are equal)
And as regard their angles, triangles may be
- Acute (all angles are acute)
- Right (one angle is right)
- Obtuse (one angle is obtuse)
- Equiangular (all angles are equal)
A triangle is scalene if all of its three sides are different (in which case, the three angles are also different). If two of its sides are equal, a triangle is called isosceles. A triangle with all three equal sides is called equilateral. S. Schwartzman's The Words of Mathematics explain the etymology (the origins) of the words. The first two are of Greek (and related) origins; the word "equilateral" is of Latin origin:
scalene (adjective): from the Indo-European root skel- "to cut." Greek skalenos originally meant "stirred up, hoed up." When a piece of ground is stirred up, the surface becomes "uneven," which was a later meaning of skalenos. A scalene triangle is uneven in the sense that all three sides are of different lengths. The scalene muscles on each side of a person's neck are named for their triangular appearance. A scalene cone or cylinder is one whose axis is not perpendicular to its base; opposite elements make "uneven" angles with the base.
isosceles (adjective): from Greek isos "equal", of unknown prior origin, and skelos "leg". The Indo-European root (s)kel- "curved, bent" is found in scoliosis and colon, borrowed from Greek. In geometry, an isosceles triangle or trapezoid has two equal legs. It may seem strange that the root means "bent" even though the sides of a triangle or trapezoid are straight, but each leg is bent relative to the adjoining legs.
equilateral (adjective): from Latin æquus "even, level," and latus, stem later-, "side," both of uncertain origin. Related borrowings from Latin are bilateral and multilateral. In geometry, equilateral triangle is one in which all sides are equal in length.
This is how the two approaches are distinguished with Venn diagrams:
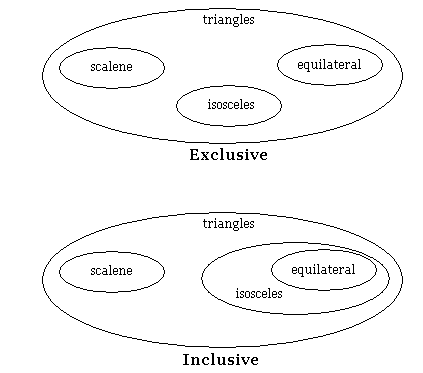
As regard the angles, a triangle is equiangular if all three of its angles are equal. Very early in the Elements (I.5 and I.6) Euclid showed that in an isosceles triangle the base angles are equal and, conversely, the sides opposite equal angles are equal. From here, for a triangle, the properties of being equilateral and equiangular are equivalent, and the latter is seldom mentioned. (For a polygon with the number of sides greater than 3 the equivalence no longer holds.)
In Euclidean geometry, the sum of the angles in a triangle equals 180°. It follows that a triangle may have at most one obtuse or even right angle. (This also follows from the Exterior Angle Theorem.) If one of the angles in a triangle is obtuse, the triangle is called obtuse. A triangle with one right angle is right. Otherwise, a triangle is acute; for all of its angles are acute. (All the definitions are naturally exclusive. There is no possible ambiguity.)
The following diagram summarizes all possible triangle configurations. The types of triangles:
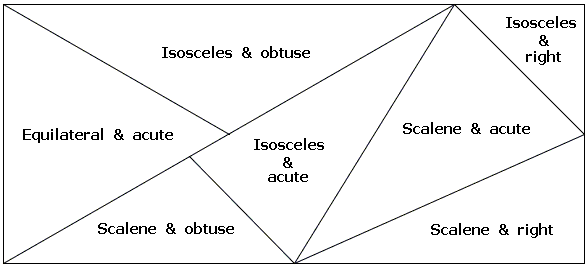
I came across this diagram in [Jacobs, p. 149] who credits First Steps in Geometry by G. A. Wentworth and G. A. Hill (Ginn, 1901).
References
- H. R. Jacobs, Geometry, 3rd edition, W. H. Freeman and Company, 2003
- S. Schwartzman, The Words of Mathematics, MAA, 1994
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73599375
