Euler Line Cuts Off Equilateral Triangle
What is this about?
A Mathematical Droodle
Problem
The applet may suggest that
In a triangle with an angle of $60^{\circ},\;$ the Euler line cuts off an equilateral triangle.
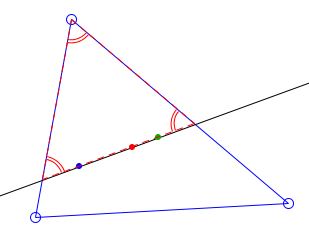
The problem comes from a Russian online journal, mat.1september.ru/2000/no43_1.htm.
For one solution, among other related facts, see a separate page.
Reformulation
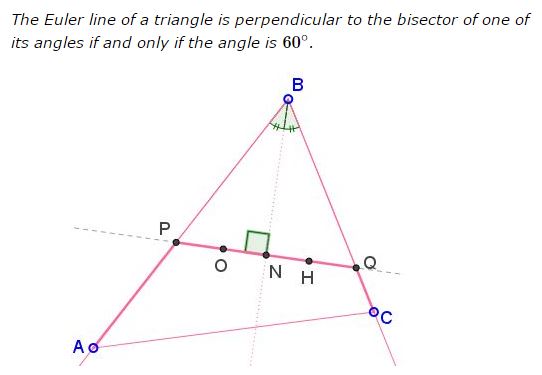
Solution
$\mathbf{If \;\angle B=60^{\circ}\; then\; HO\perp \ell_B}$
Let $O\;$ be the circumcenter, $H\;$ the orthocenter, of $\Delta ABC.\;$ Let $\ell_B\;$ be the internal angle bisector at $B,\;$ and let it cross $OH\;$ at $N.$
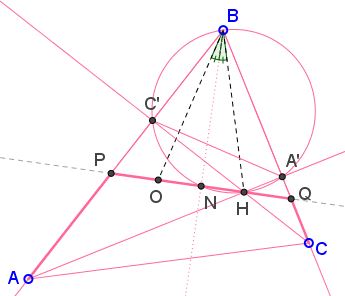
First, recollect that $H\;$ and $O\;$ are isogonal conjugate, meaning, in part, that $\angle OBN=\angle HBN.\;$ To establish the claim suffice it to show that $\Delta OBH\;$ is isosceles.
Let $AA'\;$ and $CC'\;$ be the two altitudes of $\Delta ABC.\;$ $A'C'\;$ is an antiparallel to $AC,\;$ such that the triangles $ABC\;$ and $A'BC'\;$ are similar. Now, in $\Delta AA'B,\;$ angle at $A\;$ is $30^{\circ}\;$ so that $AB=2A'B.\;$ It follows that the two triangles are similar with a coefficient of $2.\;$ In particular, the circumradius of $(ABC)\;$ is twice as large as that of $(A'BC').\;$ But, since $AA'\perp BC\;$ and $CC'\perp AB,\;$ $BH\;$ is a diameter of $(A'BC')\;$ and equals the radius $BO\;$ of $(ABC).$
$\mathbf{If\;HO\perp \ell_B\; then\; \angle B=60^{\circ}}$
We just reverse the argument.

Since $O\;$ and $H\;$ are isogonal conjugate and $OH\perp\ell_B,\;$ $\Delta OBH\;$ is isosceles: $BH=BO.\;$ But $BO\;$ is the radius of $(ABC),\;$ whereas $BH\;$ is a diameter of $(A'BC').\;$ Thus, the coefficient of similarity of the two triangles is $2,\;$ and, in particular, $2A'B=AB,\;$ such that $\angle ABA'=60^{\circ}.$
Acknowldegment
The reformulation above and the proofs are due to Ignacio Larrosa Cañestro and is a shortened translation of his web page.
- Condition to Have a 60 Degrees Angle
- Fermat in a Triangle with a 60 Degrees Angle
- Triangle with a 60 degrees angle
- Euler Line in a Triangle with a 60 Degrees Angle
- Euler Line Cuts Off Equilateral Triangle
- 9 Point Center on Angle Bisector
- Orthic Triangle in a Triangle with a 120 degrees angle
- Klamkin's Quickie via Peru Geometrico
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73555933
