Circle of Apollonius in Equilateral Triangle

The problem below has been kindly posted by Leo Giugiuc at the CutTheKnotMath facebook page. Leo credits the problem to Ruben Dario.

The problem came up in the universal language of mathematics accompanied by a diagram:

Circle of Apollonius in Equilateral Triangle, problem

Solution

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny

I shall reformulate the problem by introducing more suitable notations.

The incircle $(O)$ of an equilateral triangle $ABC$ touches $AB$ in $L$ and $AC$ in $M.$ $H$ is the midpoint of $LM.$ For $G$ on $BC,$ let $AG$ meets $(O)$ in $I$ and $J.$

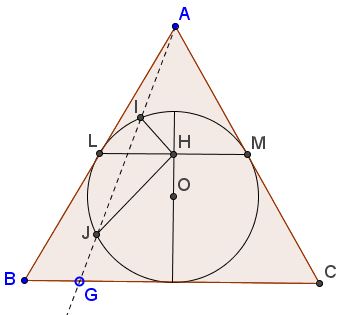
Circle of Apollonius in Equilateral Triangle, clarified problem

Prove that $4\cdot HI\cdot HJ =3r^{2},$ where $r$ is the radius of $(O).$

Solution 1

Define $E$ and $F$ as shown below:

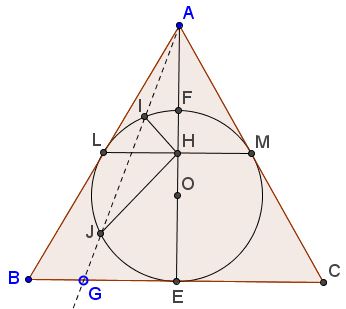
Circle of Apollonius in Equilateral Triangle, clarified problem

Due to the properties of equilateral triangle

$AF:HF=AE:HE\,(=2.)$

This means that $(O)$ is the Circle of Apollonius for points $A$ and $H,$ implying, in particular, that

$\displaystyle\frac{AI}{HI}=\frac{AJ}{HJ}=2,$

from which $AI\cdot AJ = 4\cdot HI\cdot HJ.$

On the other hand, by the Power of a Point theorem,

$\displaystyle AI\cdot AJ=AL^{2}=3r^{2}$

because $\displaystyle AL=\sqrt{3}r.$

Solution 2

This solution is based on the following observation

Let circle $(O)$ inscribed into angle $BAC$ touches side $AB$ at $L$ and side $AC$ at $M;$ let $H$ denote the midpoint of $M.$ Draw a secant $AG$ that intersects $(O)$ in $I$ and $J.$ Finally, assume $D$ is the second intersection of $JH$ with $(O).$

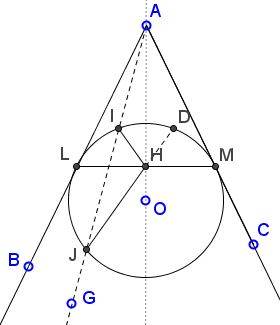
Circle of Apollonius in Equilateral Triangle, without Apollonius

Then $HI=HD.$

With this and the Intersecting Chords Theorem, the solution is immediate

$\displaystyle a\cdot b = HI\cdot HJ = HD\cdot HJ = LH\cdot MH = LH^{2}=\bigg(\frac{\sqrt{3}}{2}r\bigg)^{2}.$

Solution 3

We'll use complex numbers: $x$ will be the complex number associated with point $X.$ Let $K$ be the midpoint of $BC;$ $\displaystyle \omega = -\frac{1}{2}+i\frac{\sqrt{3}}{2}$ such that $\omega^{2}+\omega +1=0.$ Let $O$ be the origin.

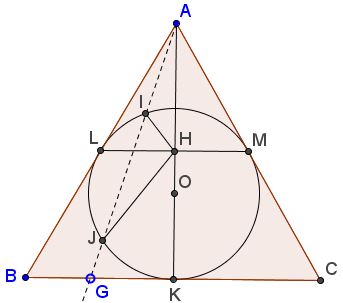
Circle of Apollonius in Equilateral Triangle, without Apollonius in comlex vars

Then $m=k\omega,$ $l=k\omega^{2}.$ Since $ALKM$ is a rhombus, $a+k=l+m=k(\omega +\omega^{2})=-k,$ implying $a=-2k.$ As the midpoint of $LM,$ $\displaystyle h=-\frac{k}{2}.$ Set also $I=ku$ and $J=kv,$ with $|u|=|v|=1.$ Then

$\begin{align}\displaystyle HI&=k\sqrt{\bigg(u+\frac{1}{2}\bigg)\bigg(\overline{u}+\frac{1}{2}\bigg)}\\ &=k\sqrt{\bigg(u+\frac{1}{2}\bigg)\bigg(\frac{1}{u}+\frac{1}{2}\bigg)}\\ &=\frac{k}{2}\sqrt{\frac{(u+2)(2u+1)}{u}}. \end{align}$

Similarly, $\displaystyle HJ=\frac{k}{2}\sqrt{\frac{(v+2)(2v+1)}{v}}.$ Thus

$\displaystyle HI\cdot HJ=\frac{k^{2}}{4}\sqrt{\frac{(u+2)(2u+1)(v+2)(2v+1)}{uv}}.$

On the other hand,

$\begin{align}\displaystyle AI&=k\sqrt{(u+2)(\overline{u}+2)}&=k\sqrt{\frac{(u+2)(2u+1)}{u}},\\ AJ&=k\sqrt{(v+2)(\overline{v}+2)}&=k\sqrt{\frac{(v+2)(2v+1)}{u}}. \end{align}$

Therefore, $\displaystyle AI\cdot AJ=k^{2}\sqrt{\frac{(u+2)(2u+1)(v+2)(2v+1)}{uv}},$ giving $4 HI\cdot HJ=AI\cdot AJ.$ It remains only to observe that, by the Intersecting Chords Theorem, $AI\cdot AJ=3r^{2}.$

Acknowledgment

Solution #2 is by René Sperb, solution #3 is by Leo Giugiuc.


Related material
Read more...

  • Equilateral Triangles on Sides of a Quadrilateral
  • Euler Line Cuts Off Equilateral Triangle
  • Four Incircles in Equilateral Triangle
  • Problem in Equilateral Triangle
  • Problem in Equilateral Triangle II
  • Sum of Squares in Equilateral Triangle
  • Triangle Classification
  • Isoperimetric Property of Equilateral Triangles
  • Maximum Area Property of Equilateral Triangles
  • Angle Trisectors on Circumcircle
  • Equilateral Triangles On Sides of a Parallelogram
  • Pompeiu's Theorem

    • |Contact| |Front page| |Contents| |Geometry| |Up|

    Copyright © 1996-2018 Alexander Bogomolny

    72505606