A Hard but Important Sangaku

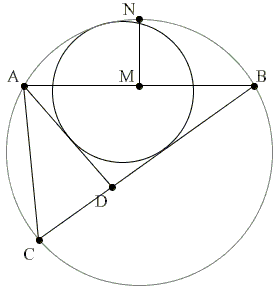
ABC is a given triangle, and circle O(R) passes through A and B, C lying within the circle. The circle O'(x) lies within O(R), touches AC and BC and also touches O(R) internally. M is the midpoint of AB and N the midpoint of the arc AB, and MN = d.

Show that

x = r + 2d(s - a)(s - b) / cs,

where s is the semiperimeter of ΔABC and r is the radius of the incircle of ΔABC.

The problem is listed as 2.2.8 by Fukagawa and Pedoe and said to be hard but important because of its relevance to a variety of other sangaku. It comes from a third volume of a 1781 collection Seiyo Sanpo by Teisi Fujita (1734-1807).

The solution below is by a New York physicist who posted it under the pseudonym yetti at the MathLinks Forums.

An alternative solution was found by James M. Unger, Professor of East Asian Languages & Literatures, The Ohio State University, Columbus, Ohio.

References

1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989, pp. 101-102

   Write to:

   Charles Babbage Research Center
   P.O. Box 272, St. Norbert Postal Station
   Winnipeg, MB
   Canada R3V 1L6

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

First extend, say, BC to cut O(R) in P:

This brings the problem into the framework of one of V. Thébault's theorems and suggests a change of notations.

Further (re)define a = BC, b = CA, c = AB, d = AD, u = BD, v = DC, where u + v = a. s = (a + b + c)/2 is semiperimeter of ΔABC; s_b = (u + c + d)/2 and s_c = (v + b + d)/2 the semiperimeters of ΔABD and ΔACD,

sb + sc = s + d.

The incenter of ΔABC will be denoted I, the incircle (I). For ΔABD, the incenter is I_b, the incircle (I_b) and the inradius r_b. We also consider the curvilinear triangles ABD and ACD with the incenters J_b and J_c and incircles (J_b) and (J_c). Note that the unknown x is the radius of (J_b).

In these notations, we want to show that

(1)	x/rb = 1 + 2·MN·(sb - u)(sb - d) / crbsb.

Using Heron's formula for ΔABD, viz.,

Area( ΔABD)² = sb(sb - u)(sb - d)(sb - c)

we transform (1) into the equivalent

(2)	x/rb - 1 = 2·MN·(sb - u)(sb - d) / crbsb   = 2·MN·(sb - u)(sb - d) / c·Area( ΔABD)   = 2·MN·Area( ΔABD) / csb(sb - c)   = 2·MN· rb / c(sb - c).

Let now T, T_b, S_b denote the points of tangency of (I), (I_b) and (J_b) with BC and Q_b that of (J_b) and AD. By Sawayama's Lemma, I, S_b and Q_b are collinear. By definition, DQ_b = DS_b, so that ΔDQ_bS_b is isosceles.

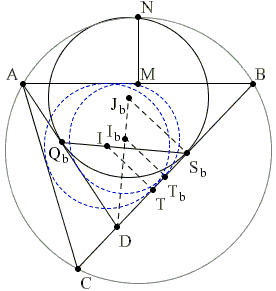
If φ = ∠ADB / 2, then ∠IS_bD = ∠IS_bT = π/2 - φ. Thus in right ΔITS_b,

TSb = IT· tan(φ) = r · tan(φ).

With this in mind,

DTb = sb - c,

whereas,

DSb = DT + TSb   = DB - TB + TSb   = u - (s - b) + r · tan(φ).

Using x = DS_btan(φ) and r_b = DT_btan(φ),

x / rb = DSb / DTb   = [u - (s - b) + r · tan(φ)] / (sb - c).

Using

u - (s - b) = u - (sb + sc - d - b)   = (sb - c) - (sc - b)

we see that

(3)	x / rb - 1 = [r · tan(φ) - (sc - b)] / (sb - c).

We have now to show that the right hand side in (3) coincides with the right hand side in (2):

[r · tan(φ) - (sc - b)] / (sb - c) = 2·MN· rb / c(sb - c)

which is the same as showing that

(4)	r · tan(φ) = 2·MN· rb / c + (sc - b).

Observe that

∠MAN = ∠BAN = ∠BCN = ∠ACB / 2

implying

2·MN / c = MN / (c/2)   = tan(∠ACB / 2)   = r / (s - c)

from ΔICT. Also, from ΔABD,

tan(φ) = rb / (sb - c),

the combination of which reduces (4) to the equivalent

(5)	rrb / (sb - c) = rrb / (s - c) + sc - b.

Using (s - c) - (s_b - c) = s - s_b = s_c - d (5) becomes

(6)	rrb(sc - d) / (sb - c)(s - c) = sc - b.

But now again r / (s - c) = tan(∠ACB / 2) = r_c / (s_c - d) which further upgrades (6) to

rbrc / (sc - b)(sb - c) = 1

which is the same as

(7)	rb / (sb - c) × rc / (sc - b) = 1.

However, r_c / (s_c - b) = tan(ψ) where ψ = ∠ADC/2. So that (7) merely asserts that tan(φ)·tan(ψ) = 1 which is obvious in view of φ + ψ = 90°.

Since (7) holds, the equivalent (1) is also true.

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
   • A Simple Solution to a Difficult Sangaku Problem
   • A Trigonometric Solution to a Difficult Sangaku Problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Chain of Circles on a Chord
21. Circles and Semicircles in Rectangle
22. Circles in a Circular Segment
23. Circles Lined on the Legs of a Right Triangle
24. Equal Incircles Theorem
    • Equal Incircle Theorem, Angela Drei's Proof
25. Equilateral Triangle, Straight Line and Tangent Circles
26. Equilateral Triangles and Incircles in a Square
27. Five Incircles in a Square
28. Four Hinged Squares
29. Four Incircles in Equilateral Triangle
    • Four Incircles in an Equilateral Triangle, a Sangaku
30. Gion Shrine Problem
31. Harmonic Mean Sangaku
32. Heron's Problem
33. In the Wasan Spirit
34. Incenters in Cyclic Quadrilateral
35. Japanese Art and Mathematics
36. Malfatti's Problem
37. Maximal Properties of the Pythagorean Relation
38. Neuberg Sangaku
39. Out of Pentagon Sangaku
40. Peacock Tail Sangaku
41. Pentagon Proportions Sangaku
42. Proportions in Square
43. Pythagoras and Vecten Break Japan's Isolation
44. Radius of a Circle by Paper Folding
45. Review of Sacred Mathematics
46. Sangaku à la V. Thebault
47. Sangaku and The Egyptian Triangle
48. Sangaku in a Square
49. Sangaku Iterations, Is it Wasan?
50. Sangaku with 8 Circles
51. Sangaku with Angle between a Tangent and a Chord
52. Sangaku with Quadratic Optimization
53. Sangaku with Three Mixtilinear Circles
54. Sangaku with Versines
55. Sangakus with a Mixtilinear Circle
56. Sequences of Touching Circles
57. Square and Circle in a Gothic Cupola
58. Steiner's Sangaku
59. Tangent Circles and an Isosceles Triangle
60. The Squinting Eyes Theorem
61. Three Incircles In a Right Triangle
62. Three Squares and Two Ellipses
63. Three Tangent Circles Sangaku
    • An Extension of a Sangaku with Touching Circles
64. Triangles, Squares and Areas from Temple Geometry
65. Two Arbelos, Two Chains
66. Two Circles in an Angle
67. Two Sangaku with Equal Incircles
68. Another Sangaku in Square
69. Sangaku via Peru
70. FJG Capitan's Sangaku

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny