Thébault's Problem III
|
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| Buy this applet What if applet does not run? |
Thébault's Problem III
The applet suggests the following theorem (Victor Thébault, 1938):
Let AM be a cevian in ΔABC, M between B and C. Construct two circles that touch BC, AM and the circumcircle of ΔABC and denote their centers as P and Q. Let I be the incenter of ΔABC. Then P, I, Q are collinear.
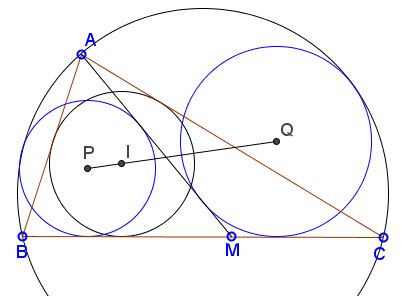
This is a problem posed by the French mathematician Victor Thébault (1882-1960) in 1938 (Amer. Math. Monthly 45 (1938), no. 7, 482-483, Advanced Problem 3887). In the English speaking world it was believed that the first solution was found by K. B. Taylor in 1983, 45 years later. (Taylor's solution occupied 24 printed pages. In [Taylor] only a summary was presented.) This much has been asserted as late as 2001 by R. Shail, himself an author of an analytic proof (Amer. Math. Monthly 108 (2001), no. 4, 319-325). However, unbeknownst to the English, in the parallel universe of the Dutch language events evolved at a faster rate. To the Dutch it took only 35 years to solve the problem. The following is an excerpt from a discussion at the geometry-college newgroup
| Subject: | Re: Do you recognize ... (Thebault's problem of 1938) |
|---|---|
| Author: | Frans Gremmen |
| Date: | 27 May 99 09:23:27 -0400 (EDT) |
Antreas P. Hatzipolakis
> The problem, published in 1938, remained
> unsolved for well over forty years until K. B. Taylor submitted a
> solution in 1983 K. B. Taylor, `Three circles with collinear
> centres',....
Some articles started with Dr. H. Streefkerk's solution of the Thebault problem in 1973. It can be found in issues of july 1973, november 1973, january 1974 and march 1974 of the Dutch magazine "Nieuw Tijdschrift voor Wiskunde".
The articles are all in Dutch. A very nice is the short one of Prof. dr. G. R. Veldkamp, it's a real beauty. It is a complete solution of Thebault's problem with some more in the issue of november 1973 p. 86-89.
Veldkamp starts from an extension of Ptolemy's theorem as follows: Instead of 4 points on a circle OMEGA, take 3 points together with a circle GAMMA tangent to OMEGA. Replace 3 of the 6 distances involved in Ptolemy's theorem by the length of the tangents from 3 points to GAMMA.
Best Regards,
Frans Gremmen, University of Nijmegen, The Netherlands.
The references below have been garnered by Bill Dubuque
Reference
- K. B. Taylor. Three circles with collinear centres, Solution of Advanced Problem 3887, Amer. Math. Monthly 90 (1983) 486-487.
- Turnwald, Gerhard. Ueber eine Vermutung von Thebault. (German) [On a conjecture of Thebault] Elem. Math. 41 (1986), no. 1, 11-13. MR 88c:51018
- Stark, R. Eine weitere Losung der Thebault'schen Aufgabe. (German) [Another solution of Thebault's problem] Elem. Math. 44 (1989), no. 5, 130-133. MR 90k:51032
- Demir, H.; Tezer, C. Reflections on a problem of V. Thebault. Geom. Dedicata 39 (1991), no. 1, 79-92. MR 92h:51029
- Rigby, John F. Tritangent centres, Pascal's theorem and Thebault's problem. J. Geom. 54 (1995), no. 1-2, 134-147. MR 96h:51014
Four years later a more complete history along with a synthetic solution has been published by the Frenchman Jean-Louis Ayme:
- J.-L. Ayme, Sawayama and Thébault's Theorem, Forum Geometricorum, v 3 (2003), 225-229,
who discovered a theorem by Y. Sawayama in an early issue of the American Mathematical Monthly (v 12 (1905), no. 12, 222-224). Sawayama's statement is in fact more general than Thébault's and the 2 page proof is entirely synthetic and elementary.
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 40618983 |
