Golden Ratio in Geometry
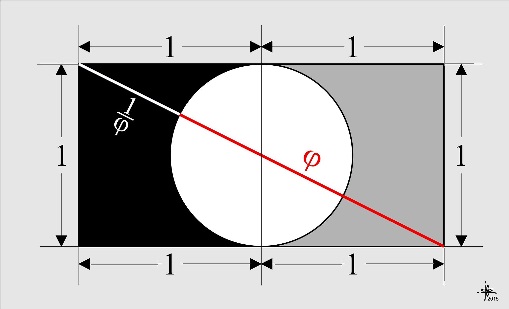
The Golden Ratio (Golden Mean, Golden Section) is defined as $\phi = (\sqrt{5} + 1) / 2.$ The classical shape based on \phi is the golden rectangle where $\phi\;$ appears alongside the perfect (unit) square:
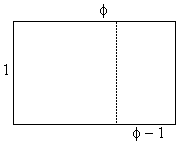
The golden rectangle has dimensions $1\times \phi\;$ such that removing the unit square one is left with the rectangle $(\phi - 1)\times 1$ similar to the original rectangle. Indeed, the most fundamental property of the golden ratio is
(1)
$\phi : 1 = 1 : (\phi - 1).$
To see this, we reduce (1) to
(2)
$\phi ^{2} - \phi - 1 = 0,$
with two solutions $(1 \pm \sqrt{5})/2$ of which one is positive and the other negative. The positive one is exactly $\phi$ while the negative is $-1/\phi.$ The reciprocal $\phi ' = 1/\phi $ is sometimes also termed the golden ratio, but more often is referred to as its conjugate. Of course also
(3)
$\phi = 1 + \phi '.$
All these equations (and an extra one) can be summarized in the following diagram [Olsen, p. 54]:
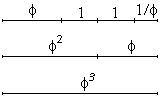
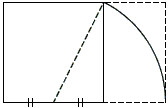
The golden rectangle is easily constructed from a square as shown in the diagram below:
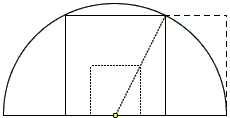
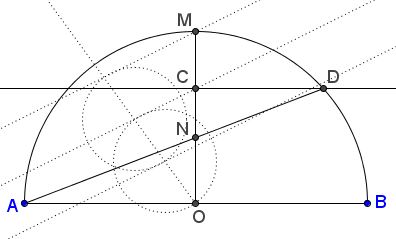
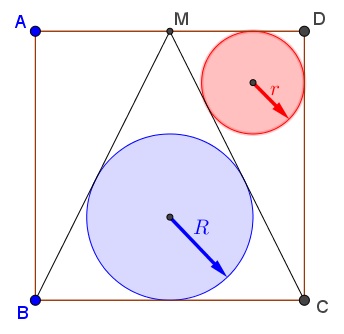
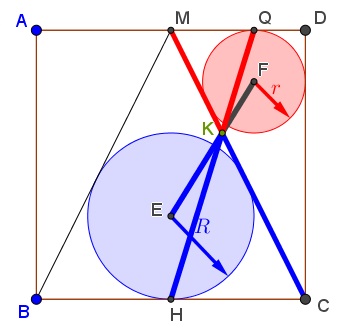
Changing the order of operations, the problem of inscribing a square into a semicircle has a golden rectangle as a biproduct. (The problem is easily solved using homothety, the same way as inscribing a square into a triangle.)
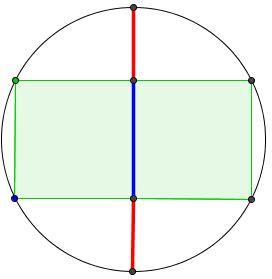
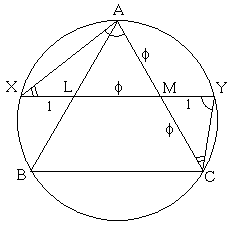
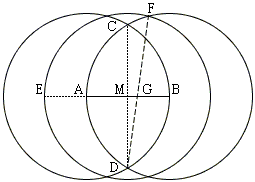
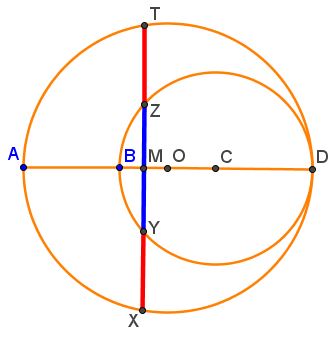
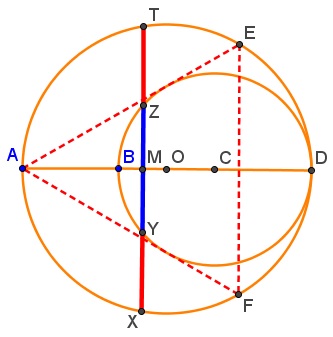
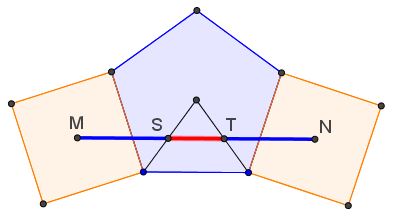
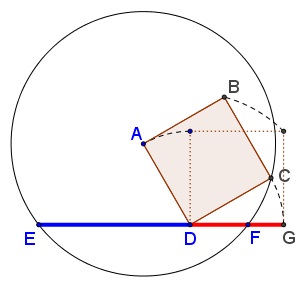
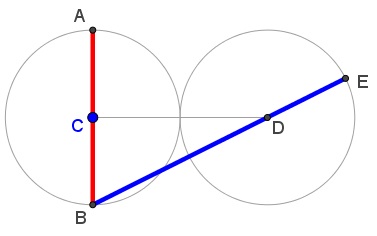
Tran Quang Hung has prepared a graphical illustration below where the ratio of the blue to a red segment is Golden.
The Golden Ratio and its inverse are roots of quadratic equations. Perhaps surprisingly, the roots of all other quadratic equations also relate to the Golden ratio (N. Lord, Golden Bounds for the Roots of Quadratic Equations, The Math Gazette, v 91, n 522, Nov. 2007, p. 549.) Indeed, let $r$ be a root of the quadratic equation $ax^{2} + bx + c = 0.$ Then the quadratic formula gives
$\displaystyle r = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a},$
from which
$\begin{align} |r| &\le (|b| + \sqrt{|b|^{2} + 4|a|\cdot|c|}) / 2|a|\\ &\le (1 + \sqrt{1 + 4}) / 2 \cdot \max\{|a|, |b|, |c|\} / |a|\\ &= \phi \cdot \max\{|a|, |b|, |c|\} / |a|. \end{align}$
The equality is of course achieved for the Golden Ratio.
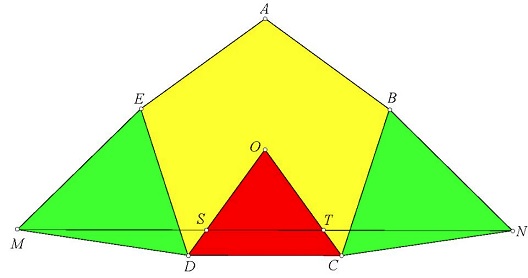
The golden ratio pops up in several geometric configurations, sometimes quite unexpectedly. It makes a stellar appearance in the pentagonal star:
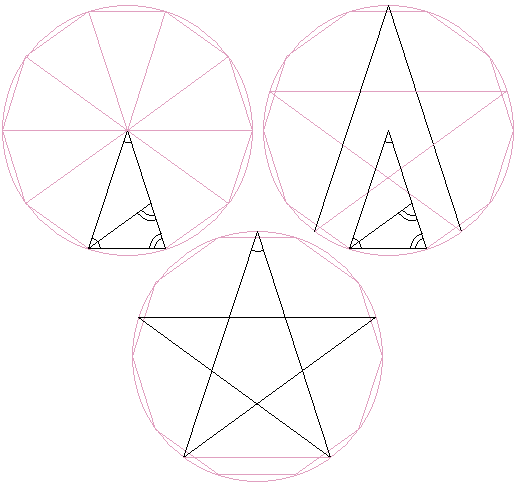
(For a more descriptive treatment check S. Brodie's construction of the pentagon and the derivation of $\cos(36^{\circ}) = (1 + \sqrt{5})/4.)$ In passing, the isosceles $72^{\circ}-36^{\circ}-72^{\circ}$ and $36^{\circ}-108^{\circ}-36^{\circ}$ triangles are known as the golden triangles because, as you see in the diagram, the bisector of a base angle in the acute one cuts off a smaller $72^{\circ}-36^{\circ}-72^{\circ}$ triangle leaving a $36^{\circ}-108^{\circ}-36^{\circ}$ one. A trisector of the apex angle of the latter divides it again into two golden triangles. In both triangles, the ratio of a big side to a small one is of course $\phi,$ what else? But this is not the only occurrence of the golden ratio in regular pentagon.
A regular pentagon can be formed by folding and tightening a narrow band of paper:
(This is the basis for my logo.)
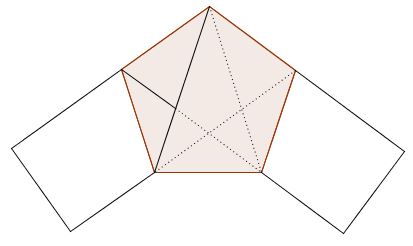
As we shall see below, the golden ratio crops up in various circumstances, often quite unexpectedly. The greatest surprise for me was to learn that a pentagon need not necessarily be regular to house all the occurrences of the golden ratio as if it were.
For the details check another page.
The golden ratio is related to the ubiquitous $ 3-4-5$ triangle [Huntley, pp. 43-44].
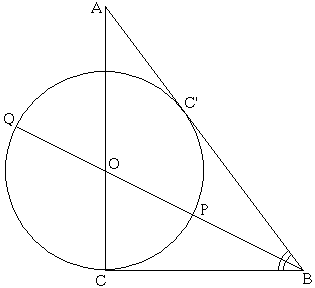
Let $ABC$ be such a triangle with $BC = 3,$ $AC = 4$ and $AB = 5.$ Let $O$ be the foot of the angle bisector at $B.$ Draw a circle with center $O$ and radius $CO.$ Extend $BO$ to meet the circle at $Q$ and let $P$ be the other point of intersection of $BO$ with the circle. Then $PQ / BP = \phi .$ For a proof, see Golden Ratio And the Egyptian Triangle.
Another way of linking the $3-4-5$ triangle to the golden ratio has been discovered by Gabries Bosia while pondering over the knight's move in chess. The latter is naturally associated with a $1:2:\sqrt{5}$ triangle. Both appear in the following diagram:
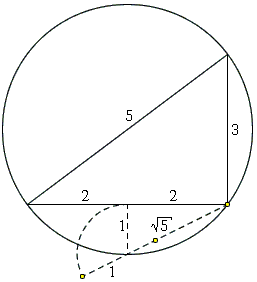
José Antônio Fabiano Mendes from Rio de Janeiro, Brazil, has observed additional appearances of the $1:2:\sqrt{5}$ triangle. The inradius of the $3-4-5$ triangle is $1$ and the distance between the incenter and the circumcenter is $\sqrt{5}/2:$
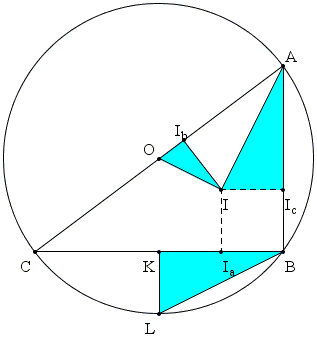
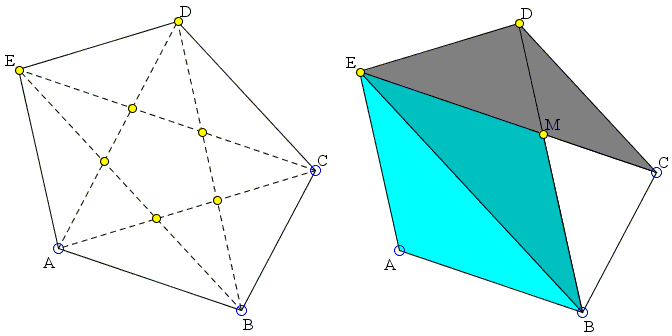
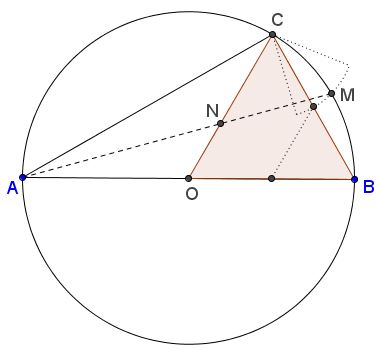
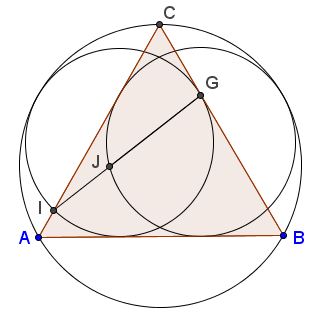
An intriguing showing of $\phi$ in an equilateral triangle was observed by George Odom, a resident of the Hudson River Psychiatric Center, in the early 1980s [Roberts, p. 10]. Upon hearing it from Odom, the late H. M. S. Coxeter submitted it as a problem to the American Mathematical Monthly (Problem E3007, 1983). The problem has also been reproduced by J. F. Rigby in [Pritchard, p. 294] and mentioned by K. Hofstetter in a recent article.
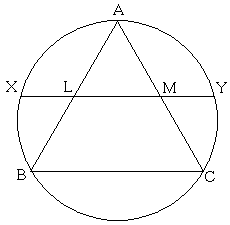
Let $L$ and $M$ be the midpoints of the sides $AB$ and $AC$ of an equilateral triangle $ABC.$ Let $X,$ $Y$ be the intersections of $LM$ extended with the circumcircle of $\Delta ABC.$ Then $LM / MY = \phi .$
Indeed, if 2a is the side length of $\Delta ABC,$ then $AM = MC = LM = a$ and $XL = MY = b.$ By the Intersecting Chords Theorem,
$MX\cdot MY = AM\cdot MC.$
In other words,
$(a + b)\cdot b = a\cdot a.$
Denoting $a/b = x,$ we see that
$1 + x = x^{2},$
which is (2), so that indeed $x = \phi.$ A derivation based on the presence of similar triangles was posted by Jan van de Craats as a solution to Coxeter's problem and included by R. Nelsen in his collection Proofs Without Words II.
(Linda Fahlberg-Stojanovska made a camcast that follows Odom's construction by paper folding a circle. The resulting pentagon is very nearly regular, but not quite.)
In the above mentioned article, K. Hofstetter, offered another elegant way of obtaining the Golden Ratio.
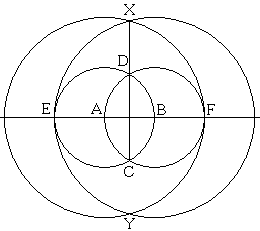
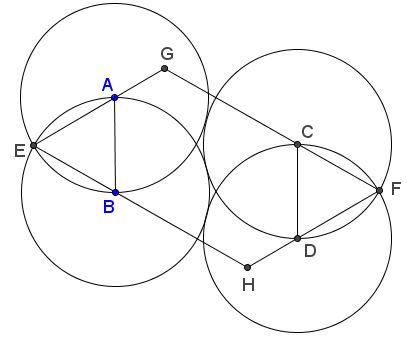
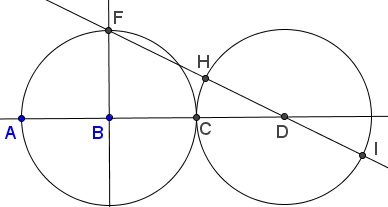
It will be convenient to denote $S(R)$ the circle with center $S$ through point $R.$ For the construction, let $A$ and $B$ be two points. Circles $A(B)$ and $B(A)$ intersect in $C$ and $D$ and cross the line $AB$ in points $E$ and $F.$ Circles $B(E)$ and $A(F)$ intersect in $X$ and $Y,$ as in the diagram. Because of the symmetry, points $X,$ $D,$ $C,$ $Y$ are collinear. The fact is $CX / CD = \phi .$ (The proof has been placed on a separate page.)
In a subsequent paper, Hofstetter gave a 5-step algorithm for dividing a segment in golden ratio:
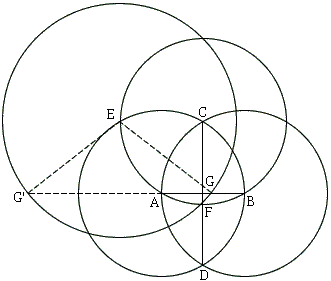
Draw $A(B)$ and $B(A)$ and let $C$ and $D$ be their points of intersection. Draw $C(A)$ and let it intersect $A(B)$ in $E$ and $CD$ in $F.$ Draw $E(F).$ This intersects the line $AB$ in points $G$ and $G'$ such that $AB:AG = \phi$ and $AG':AB = \phi.$
For a proof, suppose $AB$ has unit length. Then $CD = \sqrt{3}$ and $EG = EF = \sqrt{2}.$ Let $H$ be the orthogonal projection of $E$ on the line $AB.$ Since $HA = 1/2,$ and $HG^{2} = EG^{2} - EH^{2} = 2 - 3/4 = 5/4,$ we have $AG = HG - HA = (\sqrt{5} - 1)/2.$ This shows that $G$ divides $AB$ in the golden section.
In the third paper in the series, Hofstetter mentions having been alerted to the fact that the above proof had been discovered previously by E. Lemoine (1902) and L. Reusch (1904). The essence of the third paper is an additional 5-step division of a segment into the golden section.
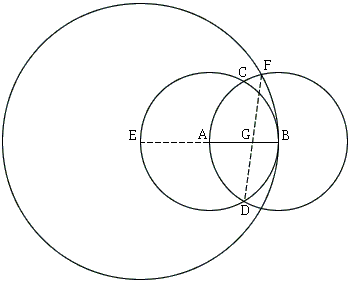
The construction is this. For a given segment $AB$ of length $1,$ form circles $A(B)$ and $B(A).$ Let $C$ and $D$ be the intersections of $A(B)$ and $B(A).$ Extend $AB$ beyond $A$ to the intersection $E$ with $A(B).$ Draw $E(B)$ and let $F$ be the intersection of $E(B)$ and $B(A)$ farther from $D.$ $DF$ intersects $AB$ in $G.$ $AG:BG = \phi .$
The diagram contains several additional occurrences of the Golden Ratio. The details have been placed in a separate page.
In a 2005 paper, Hofstetter offers a similar construction with a rusty compass whose opening can be set only once.
Draw $A(B)$ and $B(A)$ and find $C$ and $D$ at their intersection. Let $M$ be the midpoint of $AB$ found at the intersection of $AB$ and $CD.$ Construct $C(M, AB),$ a circle with center $M$ and radius $AB.$ Let it intersect $B(A)$ in $F$ and another point, $F$ being the farthest from $D.$ Define $G$ as the intersection of $AB$ and $DG.$ $G$ then is the sought point. (For details of the proof check a separate page
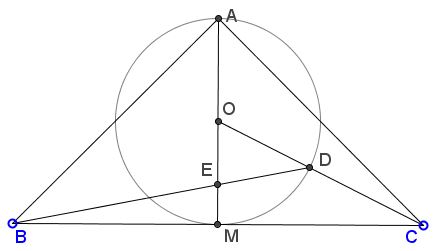
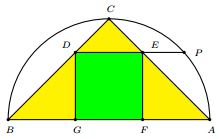
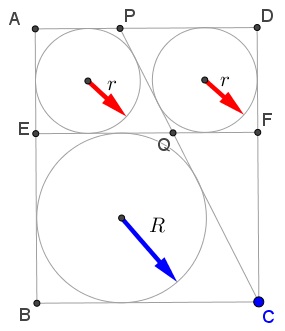
The golden ratio has been sighted in a trapezoid [Tong]. In the diagram, the bottom base $PQ$ has length $b$ and the top base $RS = a \lt b.$ The line $MN$ parallel to the bases is of length $\sqrt{(a^{2} + b^{2})/2}.$ This quantity that is known as the quadratic mean (or the root-mean-square) fits between $a$ and $b$ as any other mean would.
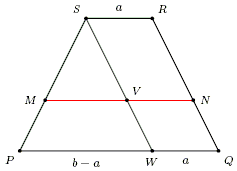
From the similarity of triangles $MSV$ and $PSW,$
$\displaystyle\frac{SM}{SP}=\frac{MV}{PW}=\frac{\sqrt{\frac{a^{2}+b^{2}}{2}}-a}{b-a}$
if $b = 3a.$ The construction of the golden ratio based on this is depicted below
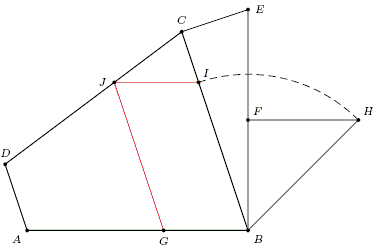
In the construction, $BC = 3\cdot AD,$ $CE = AD,$ $CE \perp BC,$ $BF = EF = FH,$ $FH \perp BE,$ $BI = BH$, $IJ\parallel AB,$ and $GJ\parallel BC.$ $AG/BG = \phi .$
The golden ratio helps resolve Curry's paradox [Gazalé, p. 133]:
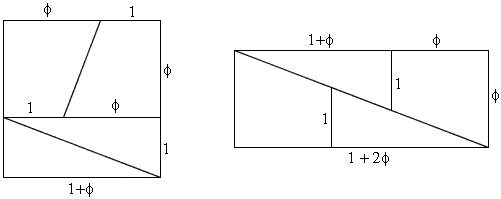
In order for the pieces to fit the rectangle tightly, from the similarity of two upper triangles we should have the proportion
$(1 + \phi ):1 = (1 + 2\phi ):\phi ,$
which is equivalent to (2). If we change units from $1$ to $5,$ we get the dissection below:

Assume the graph of a 4th degree polynomial has inflection points with abscissas $a$ and $b,$ $a \lt b.$ The straight line through the inflection points meets the graph in two other points with abscissas $x_{L}$ and $x_{R}$ say: $x_{L} \lt a \lt b \lt x_{R}.$
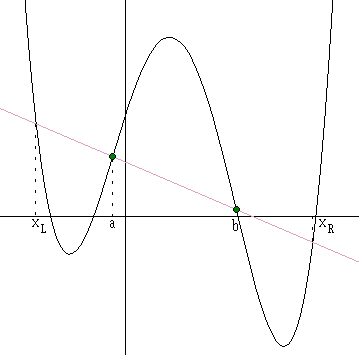
$\displaystyle x_{L}=a\frac{1+\sqrt{5}}{2} +b\frac{1-\sqrt{5}}{2}\\ \displaystyle x_{R}=b\frac{1+\sqrt{5}}{2} +a\frac{1-\sqrt{5}}{2}.$
One solution to the problem of bisecting the Yin-Yang symbol by straightedge and compass is shown in the diagram below:

The dashed line is formed by two semicircles of diameter $\phi$ and two semicircles of diameter $\phi ^{-1}.$
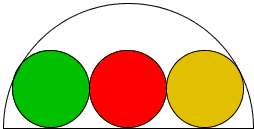
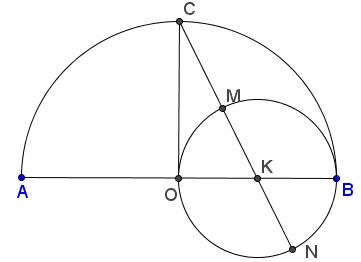
As can be easily verified, when three equal circles touch each other in sequence, and a larger semicircle, the ratio of the radius of the latter to the diameter of the small circles is $\phi.$
The only time the sides of a right triangle are in geometric progression is when the triangle is similar to the one with sides $1,$\sqrt{\phi },$ $\phi$ [Charming Proofs, p. 74]. These triangles are often referred to as Kepler's triangles.
In general, if the sides of a triangle are in geometric progression, the factor of the progression necessarily falls into the range $(1/\phi , \phi ).$
The area of annulus defined by the radii, $a$ and $b \lt a$ is equal to the area of an ellipse with major and minor axis equal to $a$ and $b,$ respectively, is when $a/b = \phi $ [Charming Proofs, p. 37].
The relation between the radii of three pairwise tangent circles that are also tangent to a line is well known
$\displaystyle\frac{1}{\sqrt{R}} = \frac{1}{\sqrt{R_{1}}} + \frac{1}{\sqrt{R_{2}}}.$
Giovanni Lucca has recently observed that the relation is actually the one that defines the Fibonacci sequence, if applied to a chain of circles standing on a straight line and tangent to their immediate members. (In the diagram below, $R_{1} = a$ and $R_{2} = b.)$
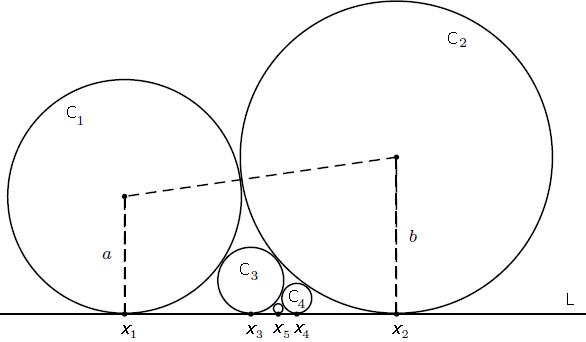
He then showed that the coordinates $x_{n}$ of the centers of the circles on the line converge to a limit $x_{\infty}$ that satisfies
$x_{\infty } - x_{1} : x_{2} - x_{\infty } = \phi \sqrt{a} : \sqrt{b}.$
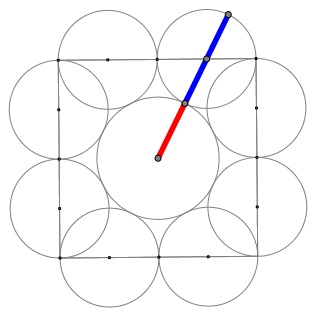
Jerzy Kocik (Math Magazine, 83 (2010) 384-390) enjoys a window in his house with an abundance of Golden Ratio and its powers. Start with two small central circles of unit diameter. The radius $R$ of the two circles on their left and right, given that a pair of congruent circles (dotted) is simultaneously tangent to all the other circles, is exactly $\phi:$
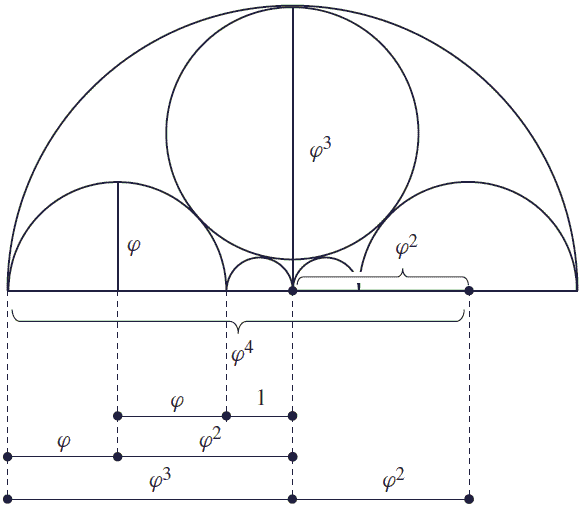
(The diagram also sports multiple appearances of the golden rectangle and Kepler's triangle.)
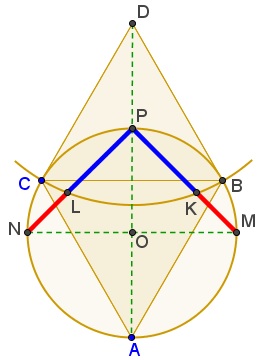
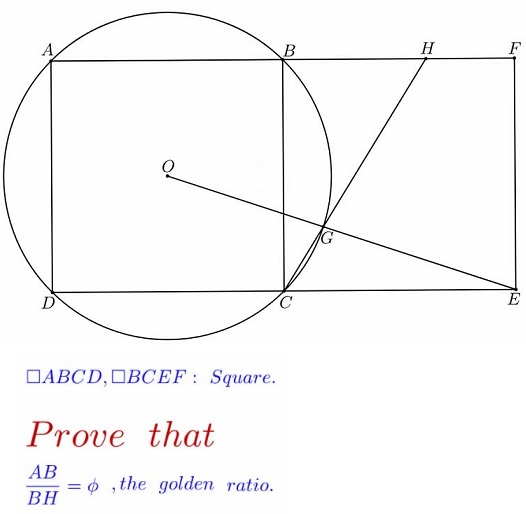
In a 2011 article, M. Bataille, offered an elegant way of constructing the Golden Ratio via an equilateral triangle and a square.

Given an equilateral triangle $ABC,$ erect a square $BCDE$ externally on the side $BC.$ Construct the circle, center $C,$ passing through $E,$ to intersect the line $AB$ at $F.$ Then, $B$ divides $AF$ in the golden ratio. (For a proof check a separate page.)
Also, in a 2011 article, Jo Niemeyer, offered a beautiful way of constructing the Golden Ratio with three equal segments, their midpoints and a pair of perpendicular lines.
Three equal segments $A_{1}B_{1},$ $A_{2}B_{2},$ $A_{3}B_{3}$ are positioned in such a way that the endpoints $B_{2},$ $B_{3}$ are the midpoints of $A_{1}B_{1},$ $A_{2}B_{2}$ respectively, while the endpoints $A_{1},$ $A_{2},$ $A_{3}$ are on a line perpendicular to $A_{1}B_{1}.$
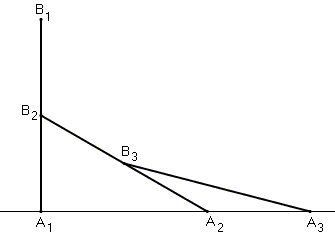
In this arrangement, $A_{2}$ divides $A_{1}A_{3}$ in the golden ratio, namely, $A_{1}A_{3} / A_{1}A_{2} = \phi .$
(For a proof check a separate page.)
Following D. MacHale (The Mathematical Gazette, v. 92, n. 525, Nov 2008, 536-537), let $\theta$ be an acute angle that solves
$\cos\theta = \tan\theta .$
(Such an angle certainly exists because graphs of the functions $y = \cos(x)$ and $y = \tan(x)$ intersect in the interval $[0, \pi /2).$ The equation is equivalent to $\cos^{2}\theta = \sin\theta ,$ or
$x^{2} + x - 1 = 0,$
with $x = \sin\theta .$ Since $|\sin\theta | \le 1,$ we have a unique solution $x = (\sqrt{5} - 1) / 2 = 1/\phi .$ It follows there is a right triangle with hypotenuse $\phi ,$ one leg $1$ and the other $\sqrt{\phi }.$ If $\theta$ is the angle opposite the leg $1,$ then $\cos\theta = \sqrt{\phi } / \phi ,$ while $\tan\theta = 1 / \sqrt{\phi },$ which are the same.
Quang Tuan Bui came up with a construction based on that of George Odom: $ABC$ and $AMN$ are two equilateral triangles where $M$ is midpoint of side $BC.$ Arc $60^{\circ}$ centered at $B$ passing through $A,$ $C$ intersects side $MN$ by golden ratio.
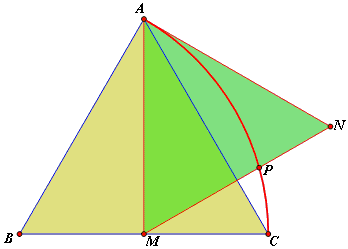
For a proof, check a separate page.
Here's another neusis construction with a proof on a separate page:
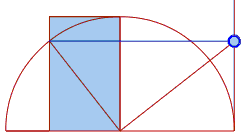
The base of the rectangle equals $1/\phi .$
John Molokach came up with a construction of the golden ratio by first constructing a golden rhombus, that is, a rhombus in which the ratio of the diagonals (long to short) equals $\phi .$
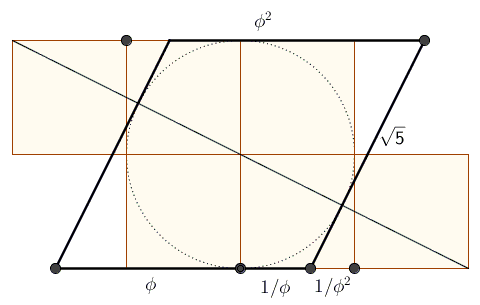
In one sweep, John additionally obtains $1/\phi ,$ $1/\phi ^{2},$ and $\phi ^{2}.$ I placed the derivation on a separate page.
Bùi Quang Tuån found a simple construction: if $\displaystyle\frac{OM}{CM}=3,$ then $\displaystyle\frac{MN}{NO}=\phi .$
I placed a proof in a separate file.
And here's one more construction from Bùi Quang Tuån. if $\displaystyle CM=\frac{BC}{2}$ then $\displaystyle\frac{CN}{NO}=\phi .$
I placed a proof in a separate file. Bùi also came up with a simple unified approach that underlies several at first sight independent construction of the Golden Ratio.
Bùi Quang Tuån has turned in another construction that is made transparent by the following diagram. $\displaystyle\frac{OE}{EM}=\phi .$
I placed a proof in a separate file.
Tran Quang Hung has contributed eight constructions of the Golden Ratio.
In a square $ABCD$, with $M,N,P,Q$ the midpoints of the sides, circle on $AP$ as diameter cuts $FN$ in Golden Ratio.
Details can be found in a separate file.
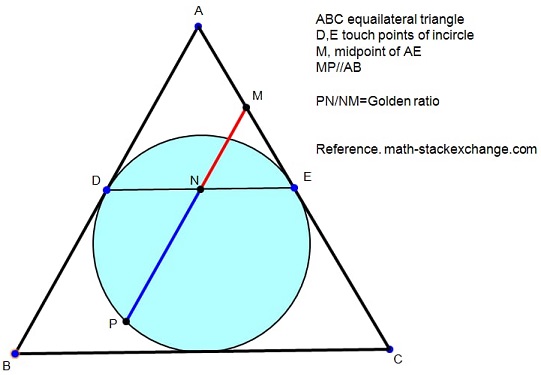
Tran's second discovery takes place in equilateral triangle.
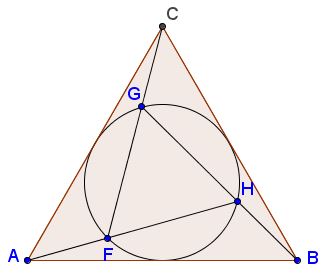
If the circumcircle $(FGH)$ of equilateral $\Delta FGH$ serves as the incircle of equilateral $\Delta ABC$ such that $F$ is on $AH,$ $G$ on $CF,$ and $H$ on $BG,$ then $F,G,H$ divide the corresponding segments $AH,CF,BG$ in Golden Ratio. Details can be found in a separate file.
Tran's third discovery relates to a hexagon:
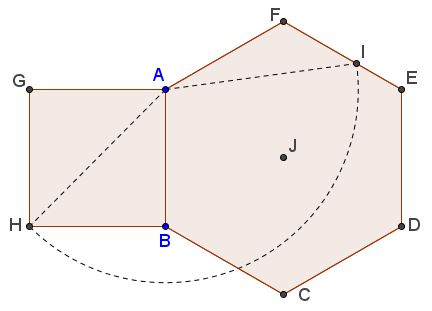
Details can be found in a separate file.
Tran's fourth construction builds on two squares $ABCD$ and $MNPC,$ with $M$ on the diagonal $BD$ (which causes $N$ to lie on $AB.)$ Let $Q$ be the intersection of $CD$ and $MP,$ extended.
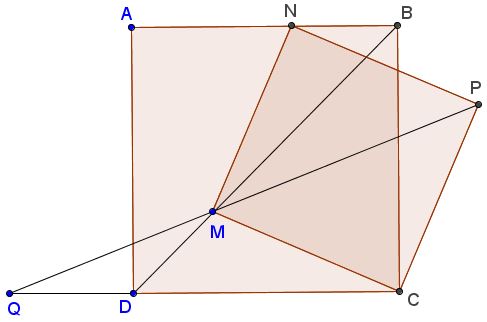
If $2DQ=CD$ then $AN/BN=\phi.$ Details can be found in a separate file.
His fifth construction starts with two equilateral triangles $ABC$ and $ABC'.$ Let $M$ be the midpoint of $BC,$ $N$ the midpoint of $AB;$ $P$ the intersection of $MN$ with the circumcircle $(ABC');$ $AP$ crosses $BC$ in $D.$
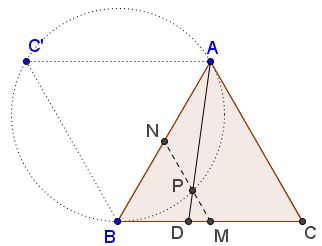
Then $CD/BD=\phi,$ the Golden Section. Details can be found in a separate file.
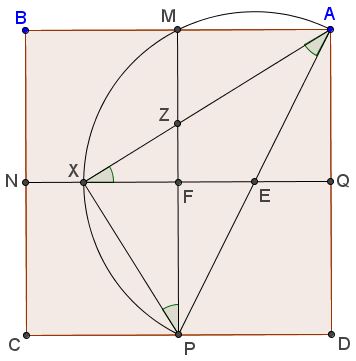
Here's Tran's sixth construction. Square $MNPQ$ is inscribed into square $ABCD$ so that the lines joining their vertices intersect the sides of $MNPQ$ at the midpoints $X,Y,Z,W,$ as shown:
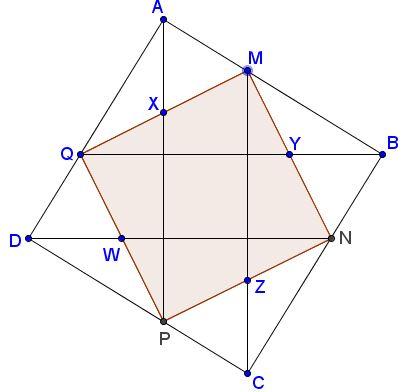
Then the vertices of $MNPQ$ divide the sides of $ABCD$ in the Golden Ratio, e.g. $\displaystyle\frac{BM}{AM}=\phi.$ Details can be found in a separate file.
Tran's seventh construction: Equilateral $\Delta DEF$ is inscribed into equilateral $\Delta ABC$ so that its extended midlines $MN, NP, MP$ pass through the vertices of $\Delta ABC,$ as shown:/p>
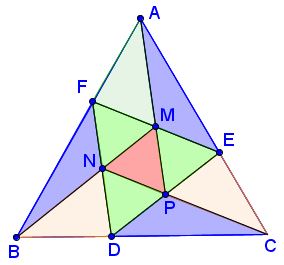
Then, say, the vertices of the inner triangle divide the sides of the outer triangle in the Golden Ratio, e.g., $\displaystyle\frac{BF}{AF}=\phi.$ Details can be found in a separate file.
Tran's construction #8: $ABCD$ is a rhombus with $2AC=BD;$ $(O)$ the inscribed circle; $E$ and $F$ the points of intersection of $(O)$ with $BD.$
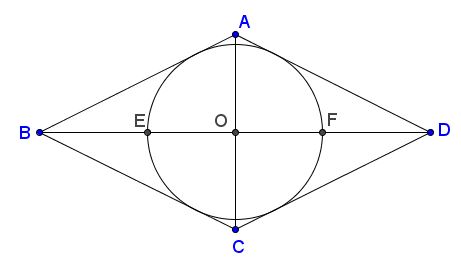
Then $F$ divides $DE$ in the golden ratio. Details can be found in a separate file.
Not to be overdone, Quang Tuan Bui devised a 5-step construction of the golden ratio:
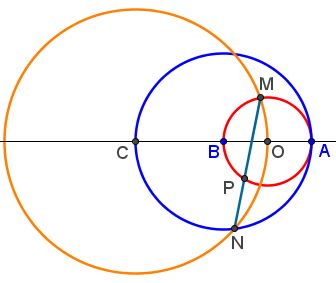
In the diagram $\displaystyle\frac{MP}{NP}=\phi.$ Details can be found in a separate file.
He also noticed an appearance of the golden ratio at the intersection of a cross and a square inscribed in the same circle:
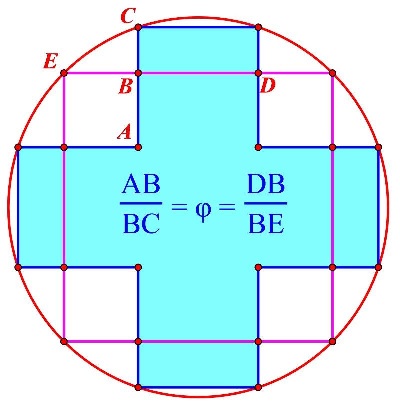
Not every cross will do but the one that consists of five equal squares. For details check a separate file
Quang Tuan Bui came up with a wonderful configuration with several instances of the Golden Ratio:
In the diagram, the sides and the diagonals of the parallelogram are in Golden Ratio; the sides are divided by the centers of the circle in Golden Ratio - but that's not all. For details check a separate file.
I've stopped getting surprised. Tran Quang Hung has found the Golden Ratio among mixtilinear circles in equilateral triangle.
Details can be found in a separate file.
In 2015 Tran Quang Hung has found once more the Golden Ratio in a combination of a semicircle, a square, and a right isosceles triangle:
Details can be found in a separate file.
Here is an invention of Elliot McGucken.
Details can be found in a separate file.
Elliot came up with another construction:
Details can be found in a separate file.
Following in Elliot's footsteps, Tran Quang Hung offered a different construction:
Details can be found in a separate file.
Tran Quang Hung and Elliot McGucken have independently came up with the following construction:
Details can be found in a separate file.
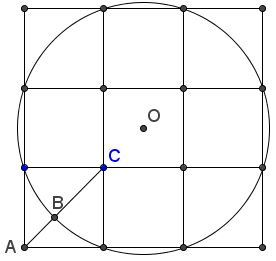
Tran Quang Hung then found another occurrence of the Golden Ratio in a $3\times 3\;$ square
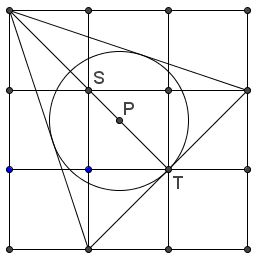
Details can be found in a separate file.
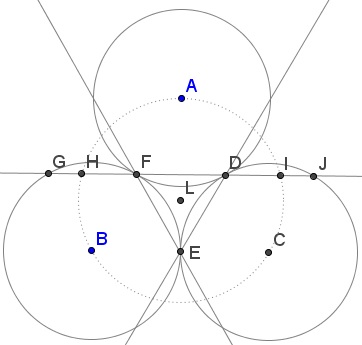
Tran Quang Hung found the Golden Ratio in three tangent circles:
Here's beautiful self-explanatory diagram by John Arioni:
The above suggests another construction:
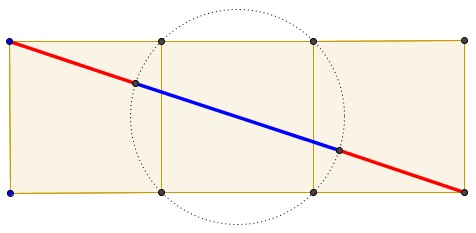
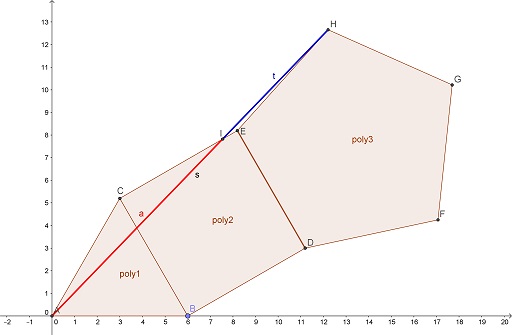
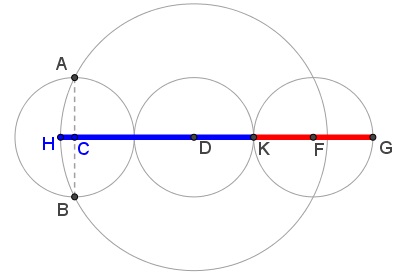
Tran Quang Hung has devised another configuration of a $1\times 3\;$ rectangle and a circle that produce The Golden Ratio. Check the ratio of the blue segment to a red one:
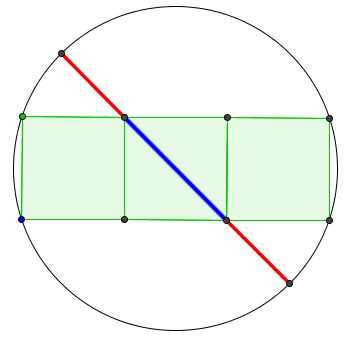
There is a not immediately obvious relation between the case of $1\times 2\;$ and $1\times 3\;$ rectangles.
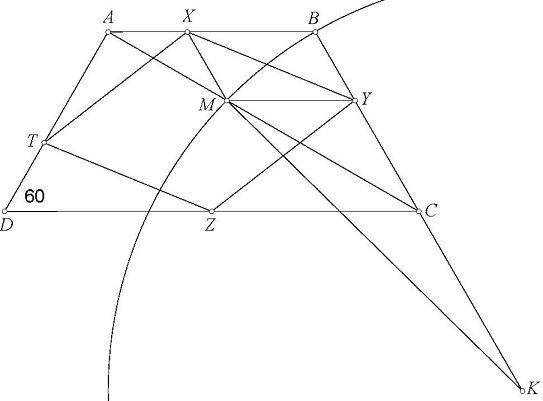
Nguyen Thanh Dung has devised the most straightforward construction of the Golden Ratio:
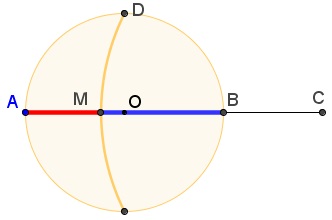
This led first to an equivalent representation formed around a $2\times 2\;$ square:
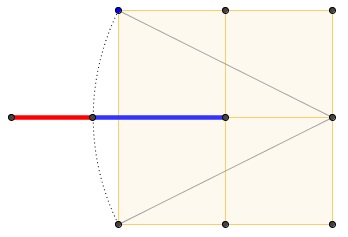
And, upon some deliberation, to the following one:
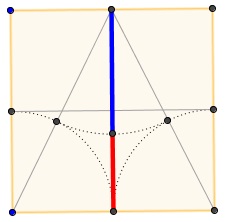
Nguyen Thanh Dung has also come up with two related constructions:
and
The latter may be confused with that of George Odom but is quite distinct.
The following construction of the Golden Ratio has been posted by Tran Quang Hung at the CutTheKnotMath facebook page.
Golden Ratio has popped up in the Odom-like constructions involving a square and a regular hexagon:
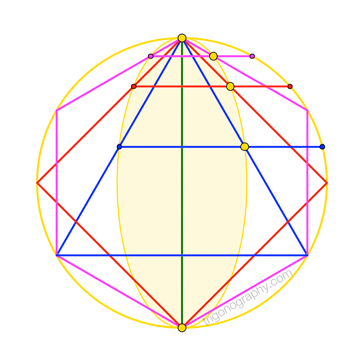
For details visit trigonography.com.
Dũng Thanh Nguyên has posted the following diagram at the CutTheKnotMath facebook page:
As there's more to it, the proof and further exploration have been placed on a separate page.
Tran Quang Hung came up with an overlooked occurrence of the Golden Ratio in a regular pentagon:
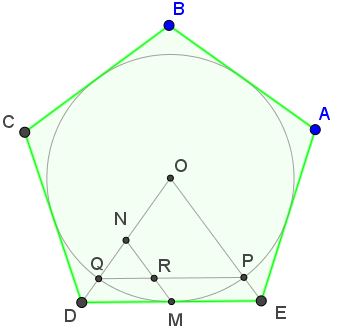
Then, $\displaystyle\frac{ON}{QN}=\frac{PR}{QR}=\varphi.\;$ The details are in a separate page.
Tran Quang Hung has found the Golden Ratio in a configuration of a regular pentagon and a regular hexagon:
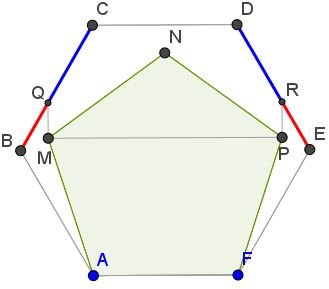
Then, $\displaystyle\frac{CQ}{BQ}=\frac{DR}{ER}=\varphi,\;$ the Golden Ratio. The details are in a separate page.
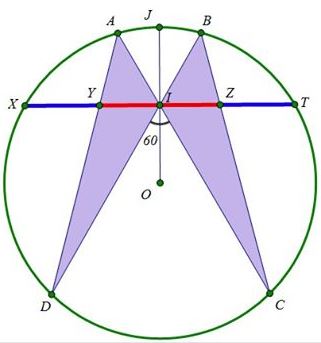
It did not take Tran Quang Hung long to find the Golden Ratio in an isosceles trapezoid with a $60^{\circ}\;$ degrees angle:
Then $\displaystyle\frac{XB}{XA}=\frac{YC}{YB}=\frac{TA}{TD}=\frac{MC}{MA}=\varphi,\;$ the Golden Ratio. The details are in a separate page.
Just in time for the festive 2016 season Tran Quang Hung found another instance of the Golden Ratio:
The details are in a separate page.
And yet another 2016 discovery by Tran Quang Hung in the nick of time, on December 31:
The details are in a separate page.
Tran Quang Hung made already several finds in 2017. Here's the first one: $\displaystyle\frac{AS}{SX}=\frac{CS}{BS}=\varphi\,$ in a mutually beneficial relationship.
The details are in a separate page.
Tran Quang Hung keeps adding to his 2017 discoveries. Reflect a regular pentagon $ABCDE\,$ in each of its sides. Join the vertices of the so obtained pentagons skipping two at a time.
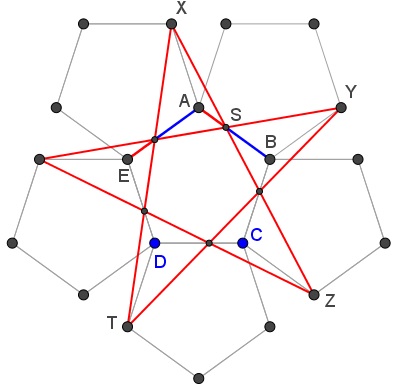
The resulting star cuts the sides of the pentagon $ABCDE\,$ in the Golden Ratio. The diagram sports additional occurrences of the Golden Ratio and other secrets.
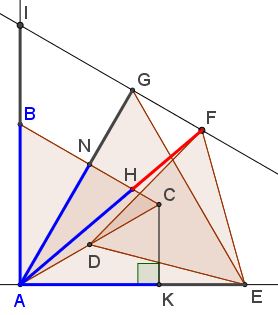
John Arioni came up with a construction of the Golden Ratio that includes $\sqrt{2},\,$ and $\pi/3:$
The details are in a separate page.
Elliot McGucken has discovered the Golden ratio in a configuration of two and three equilateral triangles, two of which are congruent:
The details are in a separate page.
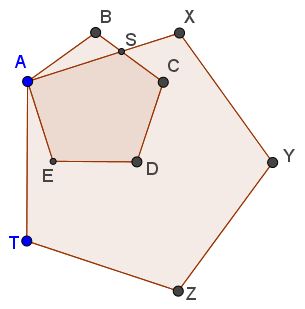
Tran Quang Hung's frequent encounters with Golden Ratio become an anticipated event. Here's he found the Golden Ratio in a configuration of three regular pentagons
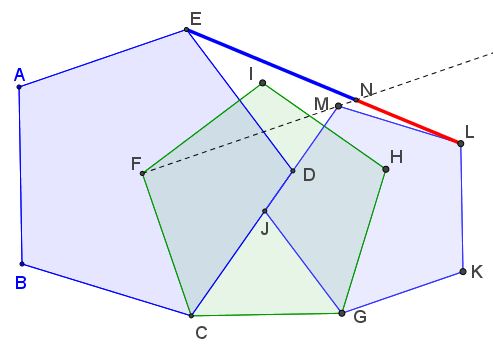
This configuration proved to conceal other instances of the glorious number:
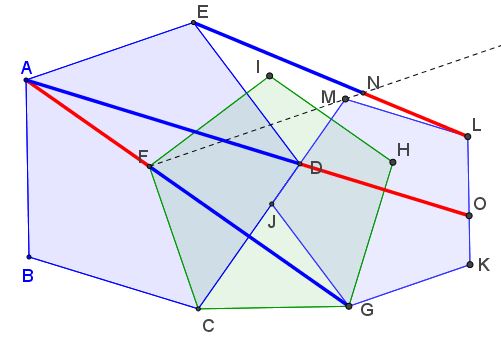
The details are in a separate page.
By changing configuration Tran Quang Hung's discovered another occurrence of the Golden Ratio. The configuration is in fact rich with pairs of segments in the Golden Ratio.
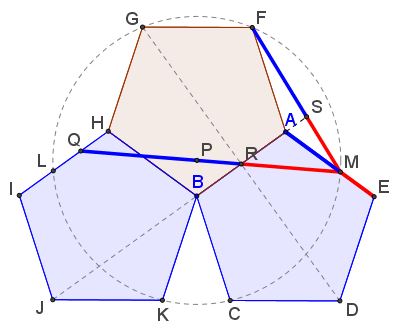
The details are in a separate page.
Replacing three regular pentagons with five equilateral triangles, Tran Quang Hung's discovered another occurrence of the Golden Ratio.
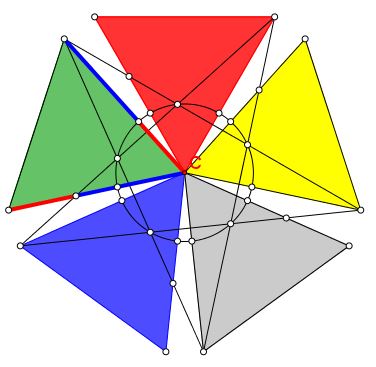
The details are in a separate page.
And another one by Tran Quang Hung:
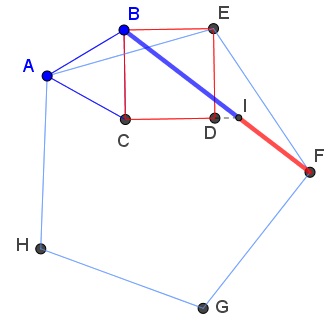
The details are in a separate file.
John Molokach has published a construction that embeds into that of John Arioni:
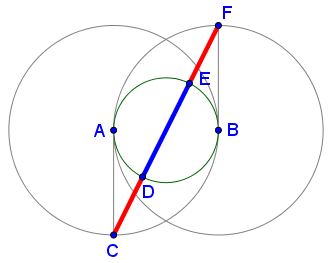
The details can be found in a separate file.
It was possible to perceive the presence of the Golden Ratio in Problem 22 from the 2014 American Mathematical Competition:
The details can be found in a separate file.
As was observed by Ercole Suppa (Italy), there's Golden Ratio in square:
and that led to other occurrences:
The details can be found in a separate file.
Kadir Altintas posted a problem at the Peru Geometrico facebook group
The details can be found in a separate file.
Kadir Altintas posted an additional problem at the Peru Geometrico facebook group
The problem reduces to George Odom's construction. The details can be found in a separate file.
Spt Ân (Vietnam) has been posted at the Peru Geometrico facebook group.
We relate this to the configuration of three squares discussed earlier. The details can be found in a separate file.
Thanos Kalogerakis came up with a construction, using three circles, which can be reduced to two:
This can be nicely modified into a construction with four circles:
The details can be found in a separate file.
Kadir Alkintas found the Golden Ratio in a special isosceles triangle but it came out squared. Ercole Suppa responded to the challenge with a construction of his own:
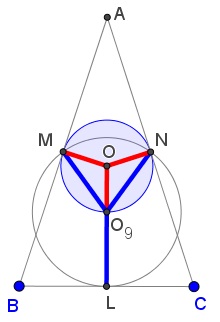
The details can be found in a separate file.
Probably there is no more appropriate place to house the Golden Ratio than the famous Yin-Yang diagram. It was John Arioni who made the discovery:
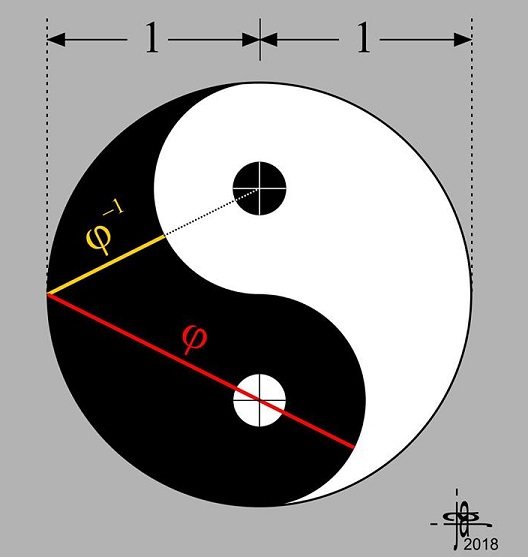
The details can be found in a separate file.
An unexpected fact has been brought to may attention by Vincent Pantaloni and to his by Coln Wright. Colin came across the diagram below at the site of Mathematics Education Innovation.
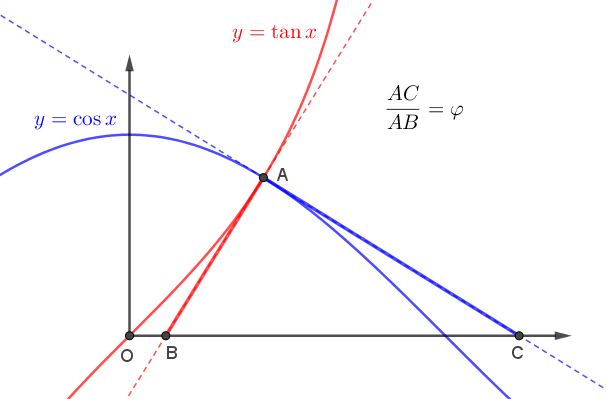
References
- C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010
- M. Bataille, Another Simple Construction of the Golden Section, Forum Geometricorum,Volume 11 (2011) 55
- M. J. Gazalé, Gnomon: From Pharaohs to Fractals, Princeton University Press, 1999
- K. Hofstetter, A Simple Construction of the Golden Section, Forum Geometricorum, v 2 (2002), pp. 65-66
- K. Hofstetter, A 5-step Division of a Segment in the Golden Section, Forum Geometricorum, v 3 (2003), pp. 205-206
- K. Hofstetter, Another 5-step Division of a Segment in the Golden Section, Forum Geometricorum, v 4 (2004), pp. 21-22
- K. Hofstetter, Division of a Segment in the Golden Section with Ruler and Rusty Compass, Forum Geometricorum, v 5 (2005), pp. 135-136
- H. E. Huntley, The Divine Proportion, Dover, 1970
- R. B. Nelsen, Proofs Without Words II, MAA, 2000
- Jo Niemeyer, A Simple Construction of the Golden Section, Forum Geometricorum, Volume 11 (2011) 53
- S. Olsen, The Golden Section: Nature's Greatest Secret, Walker & Company, 2006
- C. Pritchard (ed.), The Changing Shape of Geometry, Cambridge University Press, 2003
- S. Roberts, King of Infinite Space, Walker & Company, 2006
- J. Tong and S. Kung, A Simple Construction of the Golden Ratio, Forum Geometricorum, Volume 7 (2007) 31-32
Golden Ratio
- Golden Ratio in Geometry
- Golden Ratio in Regular Pentagon
- Golden Ratio in an Irregular Pentagon
- Golden Ratio in a Irregular Pentagon II
- Inflection Points of Fourth Degree Polynomials
- Wythoff's Nim
- Inscribing a regular pentagon in a circle - and proving it
- Cosine of 36 degrees
- Continued Fractions
- Golden Window
- Golden Ratio and the Egyptian Triangle
- Golden Ratio by Compass Only
- Golden Ratio with a Rusty Compass
- From Equilateral Triangle and Square to Golden Ratio
- Golden Ratio and Midpoints
- Golden Section in Two Equilateral Triangles
- Golden Section in Two Equilateral Triangles, II
- Golden Ratio is Irrational
- Triangles with Sides in Geometric Progression
- Golden Ratio in Hexagon
- Golden Ratio in Equilateral Triangles
- Golden Ratio in Square
- Golden Ratio via van Obel's Theorem
- Golden Ratio in Circle - in Droves
- From 3 to Golden Ratio in Semicircle
- Another Golden Ratio in Semicircle
- Golden Ratio in Two Squares
- Golden Ratio in Two Equilateral Triangles
- Golden Ratio As a Mathematical Morsel
- Golden Ratio in Inscribed Equilateral Triangles
- Golden Ratio in a Rhombus
- Golden Ratio in Five Steps
- Between a Cross and a Square
- Four Golden Circles
- Golden Ratio in Mixtilinear Circles
- Golden Ratio With Two Equal Circles And a Line
- Golden Ratio in a Chain of Polygons, So to Speak
- Golden Ratio With Two Unequal Circles And a Line
- Golden Ratio In a 3x3 Square
- Golden Ratio In a 3x3 Square II
- Golden Ratio In Three Tangent Circles
- Golden Ratio In Right Isosceles Triangle
- Golden Ratio Poster
- Golden Ratio Next to the Poster
- Golden Ratio In Rectangles
- Golden Ratio In a 2x2 Square: Without And Within
- Golden Ratio With Two Unequal Circles And a Line II
- Golden Ratio in Equilateral and Right Isosceles Triangles
- Golden Ratio in a Butterfly Astride an Equilateral Triangle
- The Golden Pentacross
- 5-Step Construction of the Golden Ratio, One of Many
- Golden Ratio in 5-gon and 6-gon
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle
- Golden Ratio in Pentagon And Two Squares
- Golden Ratio in Pentagon And Three Triangles
- Golden Ratio in a Mutually Beneficial Relationship
- Star, Six Pentagons and Golden Ratio
- Rotating Square in Search of the Golden Ratio
- Cultivating Regular Pentagons
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle II
- More of Gloden Ratio in Equilateral Triangles
- Golden Ratio in Three Regular Pentagons
- Golden Ratio in Three Regular Pentagons II
- Golden Ratio in Wu Xing
- Golden Ratio In Three Circles And Common Secant
- Flat Probabilities on a Sphere
- Golden Ratio in Square And Circles
- Golden Ratio in Square
- Golden Ratio in Two Squares, Or, Perhaps in Three
- Golden Ratio in Isosceles Triangle
- Golden Ratio in Circles
- Golden Ratio in Isosceles Triangle II
- Golden Ratio in Yin-Yang
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73558947
