Golden Ratio In a 3x3 Square

The following has been posted by Tran Quang Hung at the CutTheKnotMath facebook page, with a comment by Elliot McGucken that he made the same discovery a few days earlier. As is well known in science and mathematics, this often happens that new discoveries are often made almost simultaneously by several independent researchers.

In a $3\times 3\;$ square draw circle $(O)\;$ through the division points on the sides of the square. Let $AC\;$ be the diagonal of a corner $1\times 1\;$ square which is crossed by the circle at $B.$

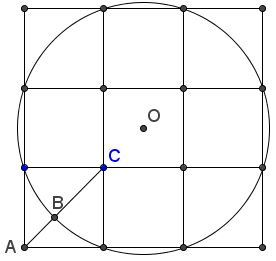
Then $B\;$ divides $AC\;$ in the Golden Ratio: $\displaystyle\frac{BC}{AB}=\varphi.$

Assume the side length of small squares is $2.\;$ Then the radius of the circle is $\sqrt{3^2+1^2}=\sqrt{10}.\;$ In particular, $OB=\sqrt{10}\;$ while $OC=\sqrt{2}\;$ and $OA=3\sqrt{2}.$ It follows that $BC=OB-OC=\sqrt{10}-\sqrt{2};\;$ $AB=OA-OB=3\sqrt{2}-\sqrt{10}.\;$ Thus we have

$\displaystyle\begin{align} \frac{BC}{AB}=\frac{\sqrt{10}-\sqrt{2}}{3\sqrt{2}-\sqrt{10}} &= \frac{\sqrt{5}-1}{3-\sqrt{5}}\\ &= \frac{(\sqrt{5}-1)(3+\sqrt{5})}{(3-\sqrt{5})(3+\sqrt{5})}\\ &=\frac{2\sqrt{5}+2}{4}\\ &=\varphi. \end{align}$

Golden Ratio

72105076