Golden Section in Two Equilateral Triangles, II

Quang Tuan Bui

November 7, 2011

ABC and AMN are two equilateral triangles where M is midpoint of side BC. Arc 60° centered at B passing through A, C intersects side MN by golden ratio.

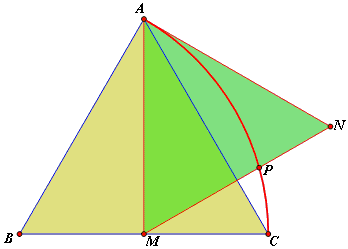
Construct two circles: circle A(P) centered at A passing through P and circle C(A) centered at C passing through A. These two circles intersect at two points. Let F denote the one that is in the same side of AC as N.

Suppose D is symmetric to A in M. Two triangles ABP and ACF are congruent because AP = AF (the radius of A(P)) and BA = BP = CA = CF (the radius of C(A)). Therefore ΔACF is obtained by a 60° rotation R(A, 60°) of ΔABP around A. This shows that ΔAPF is equilateral.

The rotation R(A, 60°) also maps ΔAMP onto ΔANF; therefore,

(1)

MP = NF

and ∠FNA = ∠PMA = ∠MAN = 60°, implying

(2)

FN||AD.

∠APD = 120° and ∠APF = 60°, so that
(3) D, P, F are collinear.

From (2) and (3) two triangles PMD, PNF are similar. Therefore:

NF/PN = MD/PM
MP/PN = NF/PN by (1)

Now we can calculate:

	x	= MP/PN = MD/PM = AM/PM = NM/PM
		= (NP + PM)/PM = NP/PM + 1 = PN/MP + 1

or x = 1/x + 1. From this x = φ, the Golden ratio.

(There is another proof for the same construction.)

Fibonacci Numbers

Golden Ratio in Geometry

72271432