Flat Probabilities on a Sphere

The probabilities in the problem are defined by the central angle $\alpha$ between the two selected points. The probability of winning is defined by the function

$\displaystyle p(\alpha)=\sin\left(\frac{\alpha}{2}\right)+\frac{1}{2}\left(\cos\left(\frac{\alpha}{2}\right)-1\right).$

The function attends its maximum for $\displaystyle\alpha_o=2\arctan(2)\approx 126.9^{\circ}.$ In addition, $\displaystyle p(\alpha_o)=\frac{1}{\varphi}=\frac{\sqrt{5}-1}{2}.$

Suppose you choose two points with central angle $\alpha.$ By symmetry we may assume they have coordinates $(0,b,c)$ and $(0,b-c).$ The diagram below shows a 2d cross section.

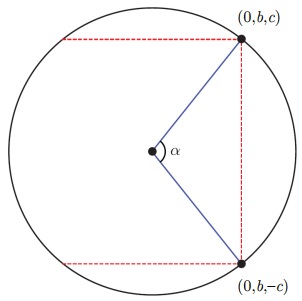
You lose your bet if your friend selects a point in one of three caps: above the plane $z=c,$ below $z=-c$ or to the right of $y=b.$

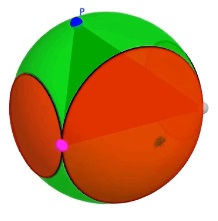
Thus, we need to compute the areas of these three spherical caps. We do that using a theorem discovered by Archimedes:

If two parallel planes $h$ units apart slice a sphere of radius $r,$ the surface area between the planes is $2\pi r h.$

Using these calculations, we conclude that the probability that you win the bet is

$\displaystyle p(\alpha)=\sin\left(\frac{\alpha}{2}\right)+\frac{1}{2}\left(\cos\left(\frac{\alpha}{2}\right)-1\right).$

The function attends its maximum for $\displaystyle\alpha_o=2\arctan(2)\approx 126.9^{\circ}.$ In addition, $\displaystyle p(\alpha_o)=\frac{1}{\varphi}=\frac{\sqrt{5}-1}{2}.$

This problem is an adaptation of Problem 305 (a Jungle Gym problem, Math Horizons n 32, 2014). The problem and the solution are by Randy Schwartz of Schoolcraft College (MN).

Steve Phelps created beautiful interactive illustrations for the problem. The latest can be accessed at the GeoGebra site; the same holds for the earlier version.