Three Equal Circles in a Semicircle

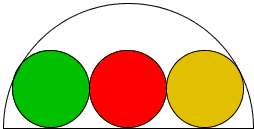
A chain of three equal circles is inscribed in a semicircle, as shown below. The ratio of the radius of the semicircle to the diameter of the small circles is the golden ratio φ.

Proof

References

C. A. Pickover, A Passion for Mathematics, John Wiley & Sons, 2005, p. 82

A chain of three equal circles is inscribed in a semicircle, as shown below. The ratio of the radius of the semicircle to the diameter of the small circles is the golden ratio φ.

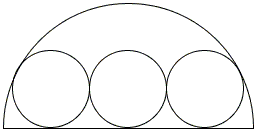
Proof

Join the centers of three circles, as shown, and extend one line to the point of tangency of two circles.

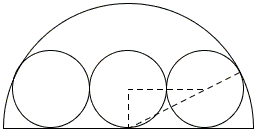
The proof needs just one application of the Pythagorean theorem. Let r and R be the radii of the small circles and the semicircle. In the right triangle in the diagram, one of the legs equals r, the other to 2r, and the hypotenuse to R - r, giving a relation:

r² + (2r)² = (R - r)²,

which translates into

R² - 2Rr - 4r² = 0.

Solving for R/r, we get

R / r = 1 ±√5.

As the minus sign would produce a negative ratio, we settle for the sign plus:

R / 2r = (1 ±√5) / 2 = φ.

41173501