Bisection of Yin and Yang

The flag of South Korea (and of Kingdom of Korea from 1883)

the flag of South Korea

contains the ancient yin-yang symbol (Taijitu in Chinese, Tomoye in Japanese and Taegeuk in Korean)

Yin and Yang

that represents the struggle, merger and co-existence of two opposites (could be hot/cold, male/female, sky/earth, moon/sun, etc.) In the diagram Yin (the negative aspect) is rendered in black, with Yang (the positive aspect) rendered in white.

The symbol is composed of two regions of a circle separated by two semicircles of half the radius of the big circle. The famous English puzzlist H. E. Dudeney posed a question [Dudeney, #158] of bisecting the Yin-Yang symbol by the common Euclidean means: straightedge and compass. He also gave two solutions: Solutions 1 and 2 below. The latter was reprinted by M. Gardner in one of his Scientific American columns and also included in two of his collections [New Mathematical Diversions, The Colossal Book of Short Puzzles]. In response to the column, several readers offered a simplification of Dudeney's proof for Solution 2. In 1960 C. W. Trigg added three more solutions (##3, 4, 5 below). Another (sixth) solution was suggested by the solution to the problem of dividing a circle into N (> 1) equal parts.

Solution 1

Yin and Yang: bisecting the two. Solution #1

This one requires no proof.

Solution 2

Yin and Yang: bisecting the two. Solution #2

Part of the Yin (black) piece below the horizontal diameter of the big circle is a semicircle with area πR²/8, where R is assumed to be the radius of the big circle, so that the small semicircle is of radius R/2. Just above the small semicircle, adjacent to the diameter is a circular sector of the big circle with central angle 45°. Its area is therefore also πR²/8. The two pieces together add to πR²/4 which is exactly half of Yin's area. It follows that the straight cut inclined 45° to the diameter, as shown, solves Dudeney's problem.

Solution 3

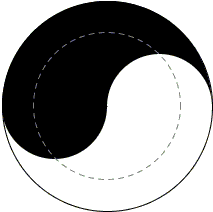
Yin and Yang: bisecting the two. Solution #3

The dashed circle has radius R/√2. Obviously, the area of the circle is πR²/2 which is then the area of the left over annulus. The rest of the proof is an easy consequence of the Carpets theorem and is continued below.

Solution 4

Yin and Yang: bisecting the two. Solution #4

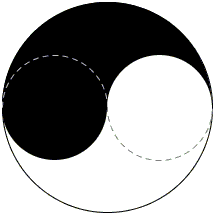
The reflection in the horizontal diameter of the big circle creates a second Yin-Yang pair of regions whose borderline supplies the necessary cut. This is an easy consequence of the Carpets theorem and is proved below. (This solution was also included into Trigg's book.)

Solution 5

Yin and Yang: bisecting the two. Solution #5

For this proof, we set x = R(√5 - 1)/4. Then the dashed line consists of two semicircles of radius x and two semicircles of radius x + R/2. It is easy to show that, for the given value of x which is incidentally half the golden ratio, the two regions into which the dashed line divides the circle have equal areas. The rest of the proof is an easy consequence of the Carpets theorem and is continued below.

Solution 6

Yin and Yang: bisecting the two. Solution #6

This is a particular case of a more general algorithm for the division of a circle into N pieces of equal areas. This is the only solution in which in addition to having equal areas the four so formed regions have also equal perimeters.

Application of the Carpet Theorem

In the solutions 3-5, let's denote the Yin/Yang regions as S₁ and S₂. The two have equal areas. In all three cases, the dashed lines divide the big circle into two regions, say T₁ and T₂, also of equal areas. Obviously, Area(T₁) = Area(S₂) and it is not important which is which. By Carpets theorem,

Area(S₁ ∩ T₁) = Area(S₂ ∩ T₂).

Observe that in all three solutions there is central symmetry with respect to the center of the big circle. Because of the symmetry, the union of the region on the left of the above equality together with the reflection of the region on the right gives either Yin or Yang, proving that the dashed line indeed divides both of them into pieces of equal areas.

Reference

H. E. Dudeney, Amuzements in Mathematics, Dover, 1970
M. Gardner, New Mathematical Diversions from Scientific American, Univ. of Chicago Press, 1983, pp. 143-146
M. Gardner, The Colossal Book of Short Puzzles and Problems, W. W. Norton & Co, 2006, pp. 126-127
C. W. Trigg, Bisection of Yin and of Yang, Mathematics Magazine, Vol. 34, No. 2 (Nov. - Dec., 1960), pp. 107-108
C. W. Trigg, Mathematical Quickies, Dover, 1985, #174

Carpets Theorem

71605951