Golden Section in Two Equilateral Triangles

Quang Tuan Bui

November 6, 2011

ABC and AMN are two equilateral triangles where M is midpoint of side BC. Arc 60° centered at B passing through A, C intersects side MN by golden ratio.

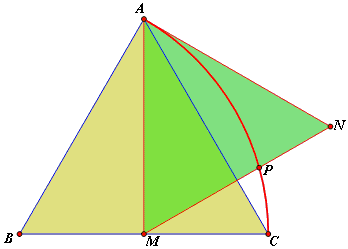
For a proof, construct

  • D as symmetry of A in M,
  • E as symmetry of A in N,
  • Q as symmetry of P in M.

By George Odom, NM/MQ = φ; therefore MN/MP = φ.

(There is another proof for the same construction.)

Fibonacci Numbers

  1. Ceva's Theorem: A Matter of Appreciation
  2. When the Counting Gets Tough, the Tough Count on Mathematics
  3. I. Sharygin's Problem of Criminal Ministers
  4. Single Pile Games
  5. Take-Away Games
  6. Number 8 Is Interesting
  7. Curry's Paradox
  8. A Problem in Checker-Jumping
  9. Fibonacci's Quickies
  10. Fibonacci Numbers in Equilateral Triangle
  11. Binet's Formula by Inducion
  12. Binet's Formula via Generating Functions
  13. Generating Functions from Recurrences
  14. Cassini's Identity
  15. Fibonacci Idendtities with Matrices
  16. GCD of Fibonacci Numbers
  17. Binet's Formula with Cosines
  18. Lame's Theorem - First Application of Fibonacci Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72338946