Golden Ratio in a Butterfly Astride an Equilateral Triangle
The following is taken from the post by Nguyên Dung Thanh at the CutTheKnotMath facebook page.
Let $J\;$ lie on circle $(O),\;$ with $I\;$ the midpoint of $OJ.\;$ Let $C,D\in (O)\;$ make $\Delta ICD\;$ equilateral. $IC, ID\;$ cut $(O)\;$ at $A, B,\;$ respectively. Let $XT\;$ be a chord through $I\;$ perpendicular to $OJ.\;$ $AD, BC\;$ cut $XT\;$ at $Y, Z,\;$ respectively. Then $\displaystyle\frac{YZ}{ZT}=\frac{YT}{YZ}=\varphi.$
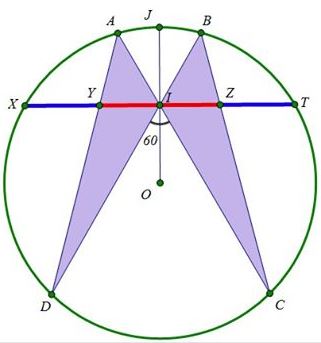
Proof
Let $OJ=1;\;$ $ID=x;\;$ $IB=y.\;$
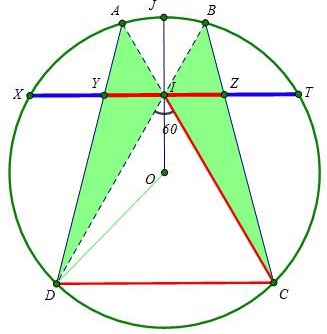
Applying the Cosine Law in $\Delta IOD,\;$ we have
$\displaystyle OD^2=OI^2+ID^2-2OI\cdot ID\cos\angle OID,$
i.e.,
$\displaystyle 1=\frac{1}{4}+x^2-2\cdot\frac{1}{2}\cdot x\cos 30^{\circ}$
from which $\displaystyle x=\frac{\sqrt{3}}{2}\frac{\sqrt{5}+1}{2}=\frac{\sqrt{3}}{2}\varphi.\;$ Hence, $CD=ID=\sqrt{3}\varphi.$
Similarly, in $\Delta OID,$
$\displaystyle OB^2=OI^2+IB^2-2OI\cdot IB\cos\angle OIB,$
i.e.,
$\displaystyle 1=\frac{1}{4}+y^2-2\cdot\frac{1}{2}\cdot y\cos 150^{\circ}$
so that $\displaystyle y=\frac{\sqrt{3}}{2}\frac{\sqrt{5}-1}{2}=\frac{\sqrt{3}}{2}\phi.\;$ Also $BD=x+y=\frac{\sqrt{15}}{2}.$
Since $IZ\parallel CD,\;$ Applying Thales' Theorem, we have
$\displaystyle IZ=CD\cdot\frac{BI}{BD}=\frac{\sqrt{3}}{2}\varphi\cdot\frac{\sqrt{3}}{2}\phi\cdot\frac{2}{\sqrt{15}}=\frac{3}{2\sqrt{15}}$
so that $YZ=2IZ=\displaystyle\frac{3}{\sqrt{15}}.\;$ Further, $\displaystyle IT=\sqrt{OT^2-OI^2}=\frac{\sqrt{3}}{2}.\;$ Hence,
$\displaystyle ZT=IT-IZ=\frac{\sqrt{3}}{2}-\frac{3}{2\sqrt{15}}=\frac{3(\sqrt{5}-1)}{2\sqrt{15}}.\;$
Finally, we obtain
$\displaystyle \frac{YZ}{ZT}=\frac{3}{\sqrt{15}}\cdot\frac{2\sqrt{15}}{3(\sqrt{5}-1)}=\frac{\sqrt{5}+1}{2}=\varphi.$
The diagram can be expanded to reveal additional occurrences of the Golden Ratio:
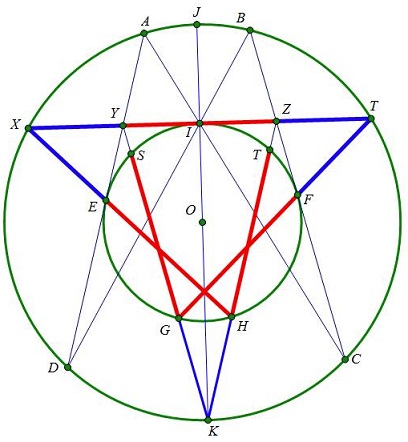
For example,
$\displaystyle\frac{TH}{HK}=\frac{EH}{EX}=\frac{YZ}{XY}=\frac{SG}{GK}=\frac{GF}{FT}=\varphi.$
Golden Ratio
- Golden Ratio in Geometry
- Golden Ratio in Regular Pentagon
- Golden Ratio in an Irregular Pentagon
- Golden Ratio in a Irregular Pentagon II
- Inflection Points of Fourth Degree Polynomials
- Wythoff's Nim
- Inscribing a regular pentagon in a circle - and proving it
- Cosine of 36 degrees
- Continued Fractions
- Golden Window
- Golden Ratio and the Egyptian Triangle
- Golden Ratio by Compass Only
- Golden Ratio with a Rusty Compass
- From Equilateral Triangle and Square to Golden Ratio
- Golden Ratio and Midpoints
- Golden Section in Two Equilateral Triangles
- Golden Section in Two Equilateral Triangles, II
- Golden Ratio is Irrational
- Triangles with Sides in Geometric Progression
- Golden Ratio in Hexagon
- Golden Ratio in Equilateral Triangles
- Golden Ratio in Square
- Golden Ratio via van Obel's Theorem
- Golden Ratio in Circle - in Droves
- From 3 to Golden Ratio in Semicircle
- Another Golden Ratio in Semicircle
- Golden Ratio in Two Squares
- Golden Ratio in Two Equilateral Triangles
- Golden Ratio As a Mathematical Morsel
- Golden Ratio in Inscribed Equilateral Triangles
- Golden Ratio in a Rhombus
- Golden Ratio in Five Steps
- Between a Cross and a Square
- Four Golden Circles
- Golden Ratio in Mixtilinear Circles
- Golden Ratio With Two Equal Circles And a Line
- Golden Ratio in a Chain of Polygons, So to Speak
- Golden Ratio With Two Unequal Circles And a Line
- Golden Ratio In a 3x3 Square
- Golden Ratio In a 3x3 Square II
- Golden Ratio In Three Tangent Circles
- Golden Ratio In Right Isosceles Triangle
- Golden Ratio Poster
- Golden Ratio Next to the Poster
- Golden Ratio In Rectangles
- Golden Ratio In a 2x2 Square: Without And Within
- Golden Ratio With Two Unequal Circles And a Line II
- Golden Ratio in Equilateral and Right Isosceles Triangles
- Golden Ratio in a Butterfly Astride an Equilateral Triangle
- The Golden Pentacross
- 5-Step Construction of the Golden Ratio, One of Many
- Golden Ratio in 5-gon and 6-gon
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle
- Golden Ratio in Pentagon And Two Squares
- Golden Ratio in Pentagon And Three Triangles
- Golden Ratio in a Mutually Beneficial Relationship
- Star, Six Pentagons and Golden Ratio
- Rotating Square in Search of the Golden Ratio
- Cultivating Regular Pentagons
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle II
- More of Gloden Ratio in Equilateral Triangles
- Golden Ratio in Three Regular Pentagons
- Golden Ratio in Three Regular Pentagons II
- Golden Ratio in Wu Xing
- Golden Ratio In Three Circles And Common Secant
- Flat Probabilities on a Sphere
- Golden Ratio in Square And Circles
- Golden Ratio in Square
- Golden Ratio in Two Squares, Or, Perhaps in Three
- Golden Ratio in Isosceles Triangle
- Golden Ratio in Circles
- Golden Ratio in Isosceles Triangle II
- Golden Ratio in Yin-Yang
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73606992
