More of Golden Ratio in Equilateral Triangles
Elliot McGucken has messaged me his discovery of the Golden Ratio in a configuration of two equal equilateral triangles and the one obtained by the addition of a third triangle. All in all, three occurrences of the Golden Ratio. The proofs by Leo Giugiuc establish the fact for the first two occurrences. From the proof of the third occurrence we derive the presence of another one.
Here's the basic configuration ($\angle BAE=90^{\circ}\,$ $AD=CD\,$ and $AC=DE):$

The first occurrence of the Golden Ratio
Let $K\,$ be on $AE\,$ with $CK\perp AE.$
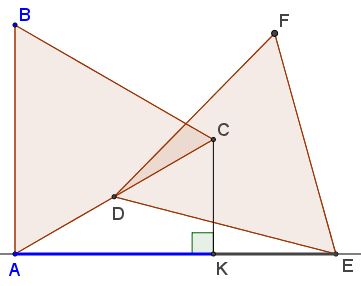
Then $\displaystyle \frac{AK}{KE}=\varphi,\,$ the Golden Ratio.
Choose $A=(0,0),\,$ $B=(0,4),\,$ then $C=(2\sqrt{3},2),\,$ $D=(\sqrt{3},1),\,$ $K=(2\sqrt{3},0).\,$ $E=(x,0).\,$ Let's find $x:\,$ $\displaystyle \left(x-\sqrt{3}\right)^2+1=16,\,$ implying $x=2\sqrt{3}\varphi\,$ and, since $AK=2\sqrt{3},\,$ $\displaystyle EK=(\varphi-1)2\sqrt{3}=\frac{2\sqrt{3}}{\varphi}.\,$ It follows that $\displaystyle \frac{AK}{AE}=\varphi.$
The second occurrence of the Golden Ratio
Let $AGE\,$ be another equilateral triangle, and $N\,$ the intersection of $BC\,$ and $AG.$
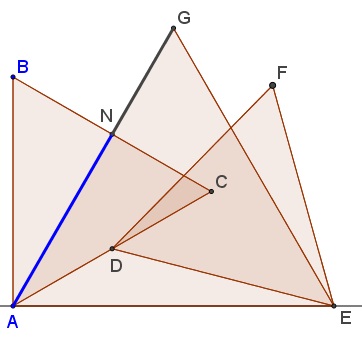
Then $\displaystyle \frac{AN}{NG}=\varphi,\,$ the Golden Ratio.
In the above notations, $G=(\sqrt{3}\varphi,3\varphi).\,$ Also, $AG\,$ is defined by $y=x\sqrt{3}\,$ whereas $BC\,$ by $x+y\sqrt{3}=4\sqrt{3},\,$ so that $N=(\sqrt{3},3).\,$ In vector notations, $\overrightarrow{AN}=\sqrt{3}\vec{i}+3\vec{j}\,$ and $\displaystyle \overrightarrow{NG}=\frac{1}{\varphi}(\sqrt{3}\vec{i}+3\vec{j}).\,$ It follows that $\displaystyle \frac{AN}{NG}=\varphi,\,$ the Golden Ratio.
The third occurrence of the Golden Ratio
Let $H\,$ be the intersection of $BC\,$ and $AF.$

Then $\displaystyle \frac{AH}{HF}=\varphi,\,$ the Golden Ratio.
Define matrix $\mathbb{M}\,$ for the clockwise rotation through $60^{\circ}:$
$\displaystyle \mathbb{M}=\frac{1}{2}\begin{pmatrix}1&\sqrt{3}\\-\sqrt{3}&1\end{pmatrix}.$
Then
$\displaystyle\begin{align} F&=E+\mathbb{M}\overrightarrow{DE}=\begin{pmatrix}2\sqrt{3}\varphi\\0\end{pmatrix}+\frac{1}{2}\begin{pmatrix}1&\sqrt{3}\\-\sqrt{3}&1\end{pmatrix}\begin{pmatrix}\sqrt{3}(1-2\varphi)\\1\end{pmatrix}\\ &=\begin{pmatrix}\sqrt{3}(1+\varphi)\\3\varphi-1\end{pmatrix}. \end{align}$
Then $AF\,$ is described with $(3\varphi-1)x-\sqrt{3}(1+\varphi)y=0.\,$ Solving this together with the equation of $BC\,$ from above $(x+y\sqrt{3}=4\sqrt{3})\,$ gives $H=(\sqrt{3}\varphi,4-\varphi).\,$ Thus, following Leo Giugiuc's footsteps, we can write
$\displaystyle\begin{align} \overrightarrow{AH}&=\sqrt{3}\varphi\vec{i}+(4-\varphi)\vec{j},\,\text{and}\\ \overrightarrow{HF}&=\sqrt{3}\vec{i}+(4\varphi-5)\vec{j}. \end{align}$
So, it is easily seen that $\displaystyle \frac{AH}{HF}=\varphi,\,$ the Golden Ratio.
The fourth occurrence of the Golden Ratio
Let $I\,$ be the intersection of $AB\,$ and $FG.$

Then $\displaystyle \frac{AB}{BI}=\varphi,\,$ the Golden Ratio.
We shall simple show that $GF\parallel BC,\,$ and applying Thales's theorem, simultaneously recovering the previous occurrence of the Golden Ratio.
Thus $B=(0,4),\,$ $C=(2\sqrt{3},2)),\,$ $G=(\sqrt{3}\varphi,3\varphi)\,$ and $F=(\sqrt{3}(1+\varphi),3\varphi-1).\,$ Thus,
$\displaystyle\begin{align} \overrightarrow{BC}&=2\sqrt{3}\vec{i}-2\vec{j},\,\text{and}\\ \overrightarrow{GF}&=\sqrt{3}\vec{i}-\vec{j}, \end{align}$
indeed implying $GF\parallel BC.$
Golden Ratio
- Golden Ratio in Geometry
- Golden Ratio in Regular Pentagon
- Golden Ratio in an Irregular Pentagon
- Golden Ratio in a Irregular Pentagon II
- Inflection Points of Fourth Degree Polynomials
- Wythoff's Nim
- Inscribing a regular pentagon in a circle - and proving it
- Cosine of 36 degrees
- Continued Fractions
- Golden Window
- Golden Ratio and the Egyptian Triangle
- Golden Ratio by Compass Only
- Golden Ratio with a Rusty Compass
- From Equilateral Triangle and Square to Golden Ratio
- Golden Ratio and Midpoints
- Golden Section in Two Equilateral Triangles
- Golden Section in Two Equilateral Triangles, II
- Golden Ratio is Irrational
- Triangles with Sides in Geometric Progression
- Golden Ratio in Hexagon
- Golden Ratio in Equilateral Triangles
- Golden Ratio in Square
- Golden Ratio via van Obel's Theorem
- Golden Ratio in Circle - in Droves
- From 3 to Golden Ratio in Semicircle
- Another Golden Ratio in Semicircle
- Golden Ratio in Two Squares
- Golden Ratio in Two Equilateral Triangles
- Golden Ratio As a Mathematical Morsel
- Golden Ratio in Inscribed Equilateral Triangles
- Golden Ratio in a Rhombus
- Golden Ratio in Five Steps
- Between a Cross and a Square
- Four Golden Circles
- Golden Ratio in Mixtilinear Circles
- Golden Ratio With Two Equal Circles And a Line
- Golden Ratio in a Chain of Polygons, So to Speak
- Golden Ratio With Two Unequal Circles And a Line
- Golden Ratio In a 3x3 Square
- Golden Ratio In a 3x3 Square II
- Golden Ratio In Three Tangent Circles
- Golden Ratio In Right Isosceles Triangle
- Golden Ratio Poster
- Golden Ratio Next to the Poster
- Golden Ratio In Rectangles
- Golden Ratio In a 2x2 Square: Without And Within
- Golden Ratio With Two Unequal Circles And a Line II
- Golden Ratio in Equilateral and Right Isosceles Triangles
- Golden Ratio in a Butterfly Astride an Equilateral Triangle
- The Golden Pentacross
- 5-Step Construction of the Golden Ratio, One of Many
- Golden Ratio in 5-gon and 6-gon
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle
- Golden Ratio in Pentagon And Two Squares
- Golden Ratio in Pentagon And Three Triangles
- Golden Ratio in a Mutually Beneficial Relationship
- Star, Six Pentagons and Golden Ratio
- Rotating Square in Search of the Golden Ratio
- Cultivating Regular Pentagons
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle II
- More of Gloden Ratio in Equilateral Triangles
- Golden Ratio in Three Regular Pentagons
- Golden Ratio in Three Regular Pentagons II
- Golden Ratio in Wu Xing
- Golden Ratio In Three Circles And Common Secant
- Flat Probabilities on a Sphere
- Golden Ratio in Square And Circles
- Golden Ratio in Square
- Golden Ratio in Two Squares, Or, Perhaps in Three
- Golden Ratio in Isosceles Triangle
- Golden Ratio in Circles
- Golden Ratio in Isosceles Triangle II
- Golden Ratio in Yin-Yang
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73561841
