Golden Ratio in Square
Problem
The following long overdue observation was proposed by Ercole Suppa (Italy) at the Peru Geometrico facebook group.
$M$ is the midpoint of side $AD$ of square $ABCD.$ Let $R$ be the inradius of $\Delta BCM,$ $r$ the inradius of $\Delta CDM.$
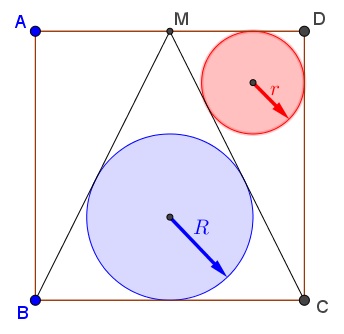
Then $\displaystyle \frac{R}{r}=\frac{\sqrt{5}+1}{2}=\varphi,$ the Golden Ratio.
Proof 1
Let $AB=2.$ Then $BM=CM=\sqrt{5}.$ We'll use a formula for the area of a triangle: the semiperimeter times the inradius. Thus, since $[\Delta BCM]=2[\Delta CDM],$
$(2\sqrt{5}+2)\cdot R=2\cdot (3+\sqrt{5})\cdot r,$
from which
$\displaystyle \frac{R}{r}=\frac{\sqrt{5}+3}{\sqrt{5}+1}=\frac{(\sqrt{5}+3)(\sqrt{5}-1)}{4}=\frac{\sqrt{5}+1}{2}=\varphi.$
Proof 2
WLOG, let $AD=2$. Let, $\angle MBC=\angle DMC=\theta$.
$\displaystyle \begin{align} &\tan \theta=\frac{2\tan \frac{\theta}{2}}{1-\tan^2 \frac{\theta}{2}}=\frac{DC}{DM}=2 \\ &\tan\frac{\theta}{2}=\frac{\sqrt{5}-1}{2}=\varphi-1.~\text{(Dropping the negative root)} \end{align}$
$\displaystyle \begin{align} \tan \angle DMF&=\tan~\frac{\theta}{2}=\frac{r}{MD-r}\\ &\Rightarrow \varphi-1=\frac{r}{1-r}\\ &\Rightarrow r=\frac{\varphi-1}{\varphi}. \end{align}$
$\displaystyle \begin{align} \tan~\angle EBC&=\tan~\frac{\theta}{2}=\frac{R}{1}\\ &\Rightarrow R=\varphi-1. \end{align}$
Thus,
$\displaystyle \frac{R}{r}=\varphi.$
Extra
We shall prove a little more, viz.,
Let $E$ and $F$ be the incenters of triangles $BCM$ and $CDM$ and $K$ the intersection of $EF$ and $CM.$
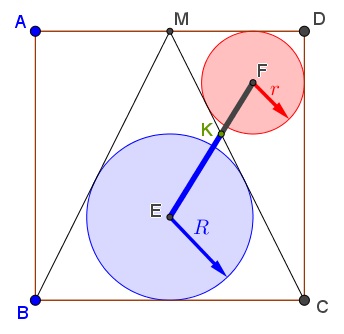
Then $\displaystyle \frac{EK}{FK}=\varphi,$ the Golden Ratio.
Proof of Extra
Let $L$ be the topmost point of $(E),$ $H$ its point of tangency with $BC$ (the midpoint of $BC),$ $P$ and $Q$ the lowest and the topmost points of $(F).$

Then, $L,K,P$ are collinear and $LP\parallel BC:$
$\displaystyle\begin{align}R&=\frac{2}{2(\sqrt{5}+1)}=\frac{\sqrt{5}-1}{4},\\ r&=\frac{1}{\sqrt{5}+3}=\frac{3-\sqrt{5}}{4},\\ ML&=2-2\cdot\frac{\sqrt{5}-1}{4}=\frac{3-\sqrt{5}}{2},\\ PQ&=2\cdot \frac{3-\sqrt{5}}{4}=\frac{3-\sqrt{5}}{2}. \end{align}$
This makes triangles $EKL$ and $FKP$ similar, so that $\displaystyle \frac{EK}{FK}=\frac{EH}{FP}=\frac{R}{r}=\varphi.$
Extra 2
Note that, from the proof above, the triangles $HKL$ and $QKP$ are also similar, so that $\displaystyle \frac{HK}{QK}=\varphi:$
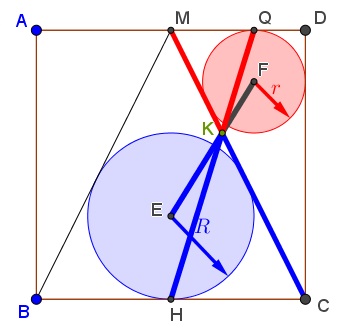
And if so, triangles $MKQ$ and $CKH$ are similar, implying $\displaystyle \frac{CK}{MK}=\varphi.$
Golden Ratio
- Golden Ratio in Geometry
- Golden Ratio in Regular Pentagon
- Golden Ratio in an Irregular Pentagon
- Golden Ratio in a Irregular Pentagon II
- Inflection Points of Fourth Degree Polynomials
- Wythoff's Nim
- Inscribing a regular pentagon in a circle - and proving it
- Cosine of 36 degrees
- Continued Fractions
- Golden Window
- Golden Ratio and the Egyptian Triangle
- Golden Ratio by Compass Only
- Golden Ratio with a Rusty Compass
- From Equilateral Triangle and Square to Golden Ratio
- Golden Ratio and Midpoints
- Golden Section in Two Equilateral Triangles
- Golden Section in Two Equilateral Triangles, II
- Golden Ratio is Irrational
- Triangles with Sides in Geometric Progression
- Golden Ratio in Hexagon
- Golden Ratio in Equilateral Triangles
- Golden Ratio in Square
- Golden Ratio via van Obel's Theorem
- Golden Ratio in Circle - in Droves
- From 3 to Golden Ratio in Semicircle
- Another Golden Ratio in Semicircle
- Golden Ratio in Two Squares
- Golden Ratio in Two Equilateral Triangles
- Golden Ratio As a Mathematical Morsel
- Golden Ratio in Inscribed Equilateral Triangles
- Golden Ratio in a Rhombus
- Golden Ratio in Five Steps
- Between a Cross and a Square
- Four Golden Circles
- Golden Ratio in Mixtilinear Circles
- Golden Ratio With Two Equal Circles And a Line
- Golden Ratio in a Chain of Polygons, So to Speak
- Golden Ratio With Two Unequal Circles And a Line
- Golden Ratio In a 3x3 Square
- Golden Ratio In a 3x3 Square II
- Golden Ratio In Three Tangent Circles
- Golden Ratio In Right Isosceles Triangle
- Golden Ratio Poster
- Golden Ratio Next to the Poster
- Golden Ratio In Rectangles
- Golden Ratio In a 2x2 Square: Without And Within
- Golden Ratio With Two Unequal Circles And a Line II
- Golden Ratio in Equilateral and Right Isosceles Triangles
- Golden Ratio in a Butterfly Astride an Equilateral Triangle
- The Golden Pentacross
- 5-Step Construction of the Golden Ratio, One of Many
- Golden Ratio in 5-gon and 6-gon
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle
- Golden Ratio in Pentagon And Two Squares
- Golden Ratio in Pentagon And Three Triangles
- Golden Ratio in a Mutually Beneficial Relationship
- Star, Six Pentagons and Golden Ratio
- Rotating Square in Search of the Golden Ratio
- Cultivating Regular Pentagons
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle II
- More of Gloden Ratio in Equilateral Triangles
- Golden Ratio in Three Regular Pentagons
- Golden Ratio in Three Regular Pentagons II
- Golden Ratio in Wu Xing
- Golden Ratio In Three Circles And Common Secant
- Flat Probabilities on a Sphere
- Golden Ratio in Square And Circles
- Golden Ratio in Square
- Golden Ratio in Two Squares, Or, Perhaps in Three
- Golden Ratio in Isosceles Triangle
- Golden Ratio in Circles
- Golden Ratio in Isosceles Triangle II
- Golden Ratio in Yin-Yang
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73603615
