Golden Ratio in a Chain of Polygons, So to Speak
Source
The following is another invention of Elliot McGucken.
Consider three regular polygons with $3,\;$ $4,\;$ and $5\;$ sides wherein all the polygons have sides of equal length throughout, as illustrated below.
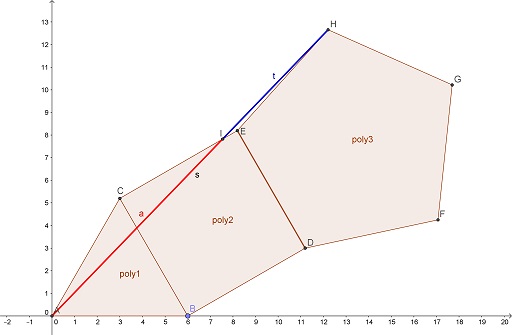
Then $\displaystyle\frac{AI}{IH}=\varphi,\;$ the Golden Ratio.
Proof
I find it convenient to turn the diagram a little as to make the axis of symmetry more pronounced:
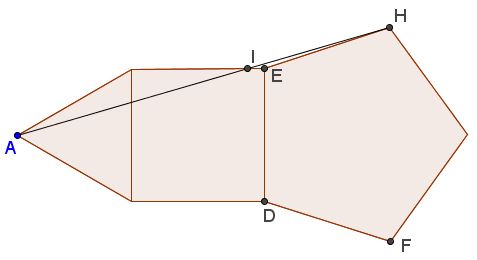
Fighting the surge to apply the power of Analytic Geometry, let's have a closer look at what has to be shown. Introduce new notations as below
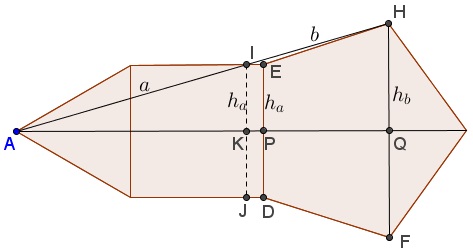
What needs to be shown is $\displaystyle\frac{a}{b}=\varphi.\;$ However, from triangles $AIK\;$ and $AHQ,\;$ $\displaystyle\frac{a+b}{a}=\frac{h_b}{h_a}=\varphi\;$ as the classical ratio of a diagonal and a side in a regular pentagon.
It follows that $\displaystyle\frac{a}{b}=\frac{1}{\varphi-1}=\varphi.$
Remark
It is interesting to observe that the presence of a triangle and a square, however visually and intellectually appealing, is much less relevant to the appearance of the Golden Ratio than that of the pentagon. Indeed, for any position of $A\;$ on the axis of symmetry of the pentagon, the ratio will be the same, provided point $I\;$ on $AH\;$ is at the same distance from the axis as the vertex $E:$
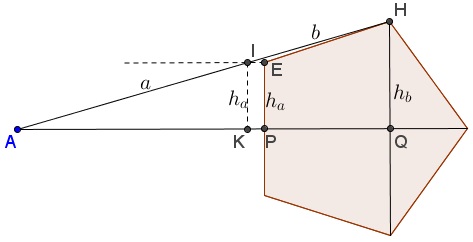
To illustrate that point and separate of what's important from what is not, Tran Quang Hung came up with the following construction: in a chain of a regular hexagon, a square, and a regular pentagon,
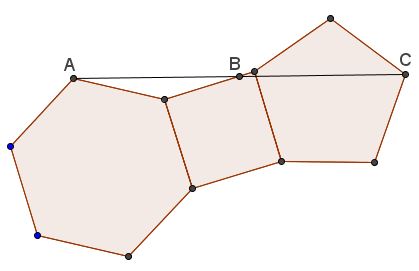
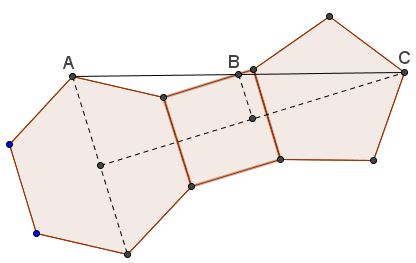
$AB=BC,\;$ and the reason is immediately clear from the following diagram by the same reasoning as above.
Tran Quang Hung has also observed that the Golden Ratio is cut off by a perpendicular bisector in a combination of a square and a regular pentagon:
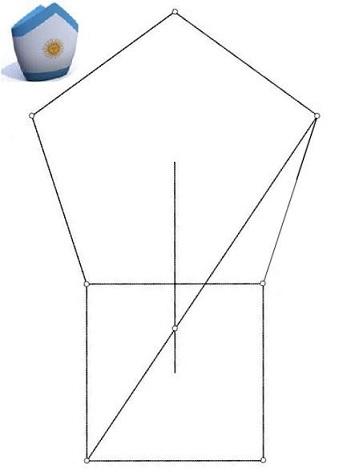
The assertion was christened "Bishop's theorem" by Gae Spes. It is clear that a rectangle can be used instead of a square.
Golden Ratio
- Golden Ratio in Geometry
- Golden Ratio in Regular Pentagon
- Golden Ratio in an Irregular Pentagon
- Golden Ratio in a Irregular Pentagon II
- Inflection Points of Fourth Degree Polynomials
- Wythoff's Nim
- Inscribing a regular pentagon in a circle - and proving it
- Cosine of 36 degrees
- Continued Fractions
- Golden Window
- Golden Ratio and the Egyptian Triangle
- Golden Ratio by Compass Only
- Golden Ratio with a Rusty Compass
- From Equilateral Triangle and Square to Golden Ratio
- Golden Ratio and Midpoints
- Golden Section in Two Equilateral Triangles
- Golden Section in Two Equilateral Triangles, II
- Golden Ratio is Irrational
- Triangles with Sides in Geometric Progression
- Golden Ratio in Hexagon
- Golden Ratio in Equilateral Triangles
- Golden Ratio in Square
- Golden Ratio via van Obel's Theorem
- Golden Ratio in Circle - in Droves
- From 3 to Golden Ratio in Semicircle
- Another Golden Ratio in Semicircle
- Golden Ratio in Two Squares
- Golden Ratio in Two Equilateral Triangles
- Golden Ratio As a Mathematical Morsel
- Golden Ratio in Inscribed Equilateral Triangles
- Golden Ratio in a Rhombus
- Golden Ratio in Five Steps
- Between a Cross and a Square
- Four Golden Circles
- Golden Ratio in Mixtilinear Circles
- Golden Ratio With Two Equal Circles And a Line
- Golden Ratio in a Chain of Polygons, So to Speak
- Golden Ratio With Two Unequal Circles And a Line
- Golden Ratio In a 3x3 Square
- Golden Ratio In a 3x3 Square II
- Golden Ratio In Three Tangent Circles
- Golden Ratio In Right Isosceles Triangle
- Golden Ratio Poster
- Golden Ratio Next to the Poster
- Golden Ratio In Rectangles
- Golden Ratio In a 2x2 Square: Without And Within
- Golden Ratio With Two Unequal Circles And a Line II
- Golden Ratio in Equilateral and Right Isosceles Triangles
- Golden Ratio in a Butterfly Astride an Equilateral Triangle
- The Golden Pentacross
- 5-Step Construction of the Golden Ratio, One of Many
- Golden Ratio in 5-gon and 6-gon
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle
- Golden Ratio in Pentagon And Two Squares
- Golden Ratio in Pentagon And Three Triangles
- Golden Ratio in a Mutually Beneficial Relationship
- Star, Six Pentagons and Golden Ratio
- Rotating Square in Search of the Golden Ratio
- Cultivating Regular Pentagons
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle II
- More of Gloden Ratio in Equilateral Triangles
- Golden Ratio in Three Regular Pentagons
- Golden Ratio in Three Regular Pentagons II
- Golden Ratio in Wu Xing
- Golden Ratio In Three Circles And Common Secant
- Flat Probabilities on a Sphere
- Golden Ratio in Square And Circles
- Golden Ratio in Square
- Golden Ratio in Two Squares, Or, Perhaps in Three
- Golden Ratio in Isosceles Triangle
- Golden Ratio in Circles
- Golden Ratio in Isosceles Triangle II
- Golden Ratio in Yin-Yang
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73561841
