Construction and Properties of Mixtilinear Incircles 2
What Might This Be About?
Problem
Given $\Delta ABC,$ construct the mixtilinear incircle inscribed into angle $B.$
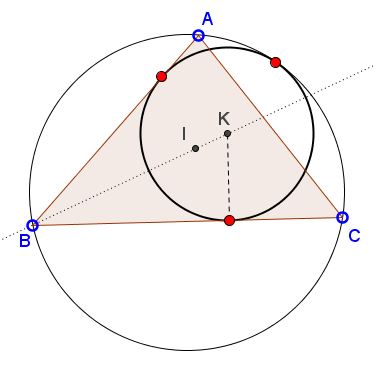
Solution
The construction proceeds in three steps:
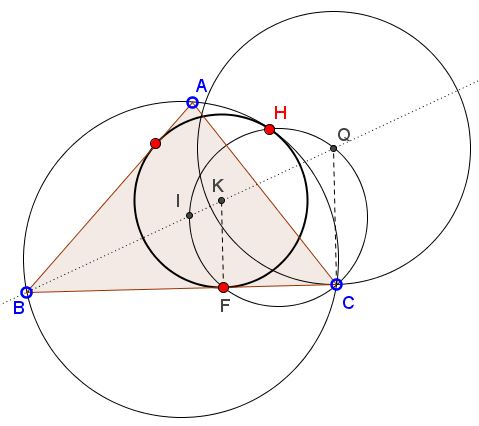
Construct circle $(Q)$ inscribed into angle $B$ and tangent to $BC$ at $C:$ draw the perpendicular to $BC$ at $C$ to its intersection at $Q$ with the angle bisector of $\angle B.$
Pass a circle through $C,$ $I$ the incenter of $\Delta ABC$, and $Q.$ Find $F$ - its second intersection with $BC.$
Errect the perpendicular at $F$ to $BC$. Its point of intersection $K$ with the bisector of $\angle B$ is the center of the sought mixtilinear circle.
Proof
By the Power of a Point Theorem, $BF\cdot BC=BI\cdot BQ.$ Obviously, $\displaystyle\frac{BQ}{BI}=\frac{c}{p-b},$ where, as usual, $a,b,c$ are the side lengths of $\Delta ABC$ and $p$ its semiperimeter. We also know that $BI^{2}=\displaystyle\frac{(p-b)ac}{p}.$ From here,
$BF=BI^{2}\displaystyle\frac{1}{p-b}=\frac{ac}{p},$
exactly the expression for the point of tangency of the mixtilinear circle with $BC.$
Extra
The second point of intersection of $(CIQ)$ with the circumcircle $(ABC)$ - $H$ in the diagram below, is the point of tangency of the circumcircle and the mixtilinear circle $(K).$ In other words, points $H,$ $K,$ and the circumcenter $O$ are collinear.

Acknowledgment
The construction has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575985
