Golden Ratio in Two Equilateral Triangles

Here's a slight modification of a construction of the Golden Ratio posted by Tran Quang Hung (with a proof) at the CutTheKnotMath facebook page.

Construction

Given two equilateral triangles $ABC$ and $ABC',$ $M$ the midpoint of $BC,$ $N$ the midpoint of $AB;$ $P$ the intersection of $MN$ with the circumcircle $(ABC');$ $AP$ crosses $BC$ in $D.$

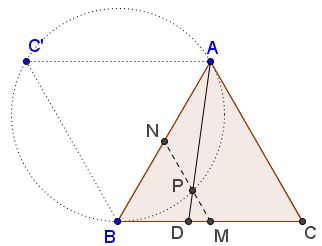
golden ratio by Tran Quang Hung, construction #5

Then $CD/BD=\phi,$ the Golden Section.

Proof

Let $E$ be the intersection of $BP$ and $AC.$ The arc of $(ABC')$ within $\Delta ABC$ is $120^{\circ}$ and both $BC$ and $AC$ are tangent to $(ABC').$

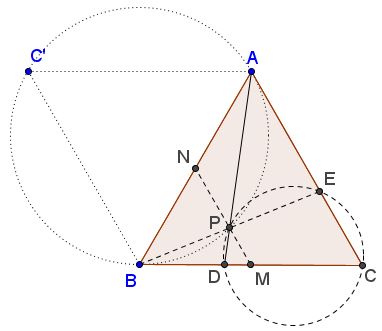
golden ratio by Tran Quang Hung, construction #5, proof

Since $\angle DCE +\angle DPE=180^{\circ},$ quadrilateral CDPE is cyclic. Now, triangles $BDP$ and $ADB$ are similar. So, $PB.AD=BD.BA=BD.BC=BP.BE,$ implying $AD=BE$ from which $\Delta ABE= \Delta CAD.$ Thus, $CD=AE.$ Further, $BD.BC=BP.BE=EP.EB=EA^2=CD^2$ which gives $DB/DC=CD/CB,$ a characteristic property of the Golden Section.

Golden Ratio

49552199