Golden Ratio in Hexagon

Tran Quang Hung has posted on the CutTheKnotMath facebook page a simple construction of the golden ratio in hexagon.

Construction

Square $ABHG$ is constructed outside the hexagon $ABCDEF.$ Circle $(A, CH)$ with center at $A$ and radius $AH$ cuts $EF$ at $I$ in Golden Ratio:

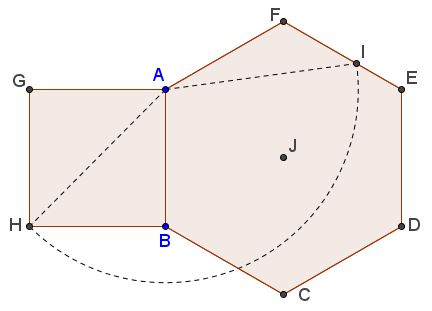
golden ratio by Tran Quang Hung, construction #3

Proof

Assume, without loss of generality, that $AB=AF=1.$ Then $AI=AH=\sqrt{2}.$

Set $\alpha = \angle FAI,$ $\beta =\angle AIF.$ Apply the Law of Sines in $\Delta AIF:$

$\displaystyle\frac{AF}{\sin\beta}=\frac{FI}{\sin\alpha}=\frac{AI}{\sin 120^{\circ}}.$

This can be rewritten as

$\displaystyle\frac{1}{\sin\beta}=\frac{FI}{\sin\alpha}=\frac{\sqrt{2}}{\sqrt{3}/2}=\frac{2\sqrt{6}}{3}.$

Thus we can identify $\beta:$ $\displaystyle\sin\beta=\frac{\sqrt{6}}{4}.$ Next we compute $\displaystyle\cos\beta=\frac{\sqrt{10}}{4}.$ Now, observe that $\alpha +\beta =60^{\circ},$ so that

$\begin{align}\displaystyle \sin\alpha &= \sin (60^{\circ}-\beta)\\ &= \sin 60^{\circ}\cdot\cos\beta-\cos 60^{\circ}\cdot\sin\beta\\ &=\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{10}}{4}-\frac{1}{2}\cdot\frac{2\sqrt{6}}{3}\\ &=\frac{\sqrt{6}}{8}(\sqrt{5}-1). \end{align}$

From here

$\displaystyle FI = \sin\alpha\cdot\frac{2\sqrt{6}}{3}=\frac{\sqrt{6}}{8}(\sqrt{5}-1)\cdot\frac{2\sqrt{6}}{3}=\frac{\sqrt{5}-1}{2}=\frac{1}{\phi}.$

It follows that $\displaystyle\frac{EF}{FI}=\frac{FI}{EI}=\phi.$

A proof using Stewart's Theorem has been suggested by Leo Giugiuc. Apply Stewart's theorem to $\Delta AEF$ and the cevian $AI:$

$AF^{2}\cdot EI+AE^{2}\cdot FI=AI^{2}\cdot EF+EI\cdot FI\cdot AF.$

Substituting $AF=EF=1,$ $AI=\sqrt{2},$ $AE=\sqrt{3},$FI=x,$ $EI=1-x$ gives

$(1-x)+3x=2+(1-x)x.$

This reduces to the quadratic equation $x^{2}+x-1=0,$ with the only positive solution $\displaystyle x=\frac{\sqrt{5}-1}{2},$ which gives $1-x=\displaystyle\frac{3-\sqrt{5}}{2},$ and, finally, $\displaystyle\frac{x}{1-x}=\phi.$

Remark

Tran Quang Hung's construction that employs the diagonal of a square as a radius of a circle is akin to that of M. Bataille. Here's two constructions in the same diagram:

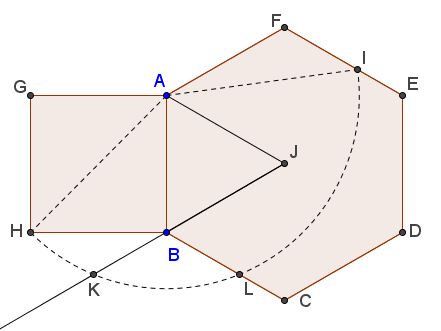
golden ratio by Tran Quang Hung and M. Bataille - comparison

According to M. Bataille, $\displaystyle\frac{BJ}{BK}=\phi;$ according to Tran Quang Hung, $\displaystyle\frac{BL}{CL}=\frac{FI}{EI}=\phi.$

A 2011 article by Quang Tuan Bui covers both cases and leads to a whole family of Golden Ratios in a regular hexagon. Tran Quang Hung's construction, like that of M. Battaille, has been discovered independently.

Golden Ratio

72193030