A Modified Sangaku
Source
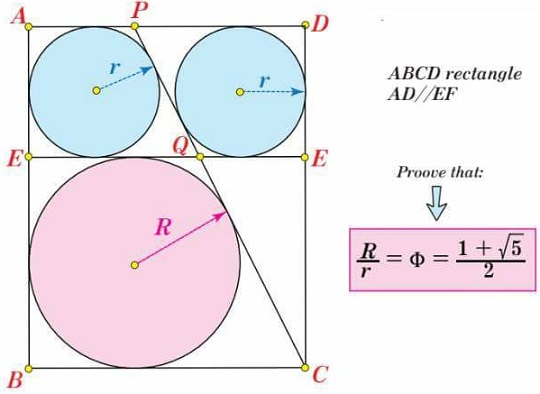
Problem
In rectangle $ABCD,$ $E\in AB,$ $F\in CD,$ $EF\parallel BC;$ $P\in AD;$ $Q=CP\cap EF.$
Each of the quadrilaterals $AEQP,$ $DPQF,$ and $BCQE$ is inscriptible, the former two are equal.
If $r$ is the common radius of the incircles of $AEQP$ and $DPQF,$ and $R$ the inradius of $BCQE,$ prove that $\displaystyle \frac{R}{r}=\varphi,$ the Golden Ratio.
Solution
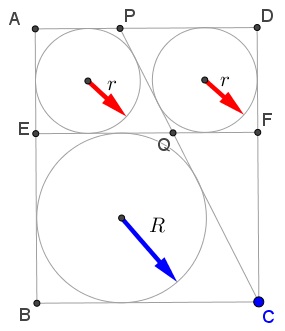
Extend $CP$ and $BA$ to the cross-point $K:

Obviously, line $PQ$ passes through the center of the rectangle $AEFD.$ That point projects to the midpoint of $BC,$ implying that it is also the midpoint of $KC.$ Thus, $BE=AK=2R$ and $AE=2r.$ The incircle of $BCQE$ serves as the incircle of $\Delta BCK$ while the incircle of $AEQP$ is the incircle of $\Delta EQK.$ We thus have the proportion:
$\displaystyle \frac{BK}{EK}=\frac{4R+2r}{2R+2r}=\frac{R}{r},$
giving an equality $\displaystyle (2R+r)r=(R+r)R,$ or, $R^2-Rr-r^2=0,$ from which $\displaystyle \frac{R}{r}=\frac{\sqrt{5}+1}{2}.$
Extra
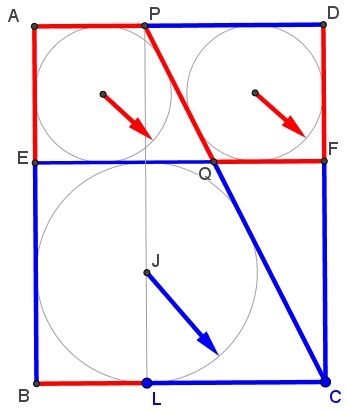
As the consequence of the above, it is easily seen that the configuration sports multiple occurrences of the Golden Ratio, as is illustrated below.
Acknowledgment
The problem has been posted by Kadir Altintas at the Peru Geometrico facebook group, with a reference to Géry Huvent note Sangaku.
Several additional solutions can be found by following the link above to the Peru Geometrico.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73608097
