Golden Ratio in a Mutually Beneficial Relationship
Problem
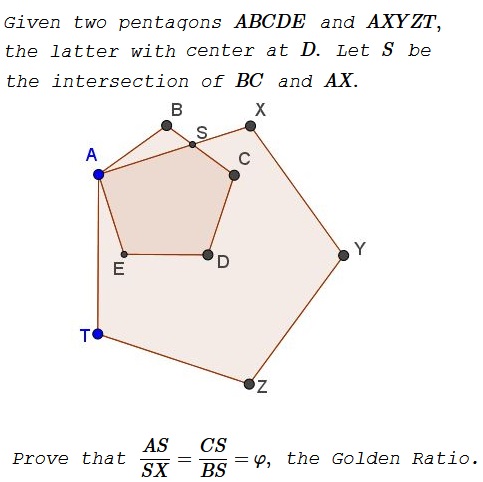
Solution 1
We start with a
Lemma
If $u=e^{\frac{2\pi i}{5}},\,$ then $\varphi =-u^2-u^3.$
Indeed,
$\displaystyle\begin{align} -u^2 &=-\cos\frac{4\pi}{5}-i\sin\frac{4\pi i}{5}=\cos\frac{\pi}{5}-i\sin\frac{\pi i}{5}\\ &=\frac{\varphi}{2}-i\sin\frac{\pi}{5} \end{align}$
and
$\displaystyle\begin{align} -u^3 &=-\cos\frac{6\pi}{5}-i\sin\frac{6\pi i}{5}=\cos\frac{\pi}{5}+i\sin\frac{\pi i}{5}\\ &=\frac{\varphi}{2}+i\sin\frac{\pi}{5} \end{align}$
Adding the two proves the lemma.
To continue, choose $D=1,\,$ $C=u,\,$ $B=u^2,\,$ $A=u^3.\,$ We have $\displaystyle\frac{A-D}{X-D}=u=\frac{1}{u^4},\,$ implying $\displaystyle\frac{u^3-1}{X-1}=\frac{1}{u^4},\,$ i.e., $X=1+u^2-u^4\,$ (all because $u^5=1).\,$ It follows that $X-B=1-u^4.\,$ By the lemma,
$\varphi(X-B)=(u^2+u^3)(u^4-1)=u-u^3=C-A,$
such that $AC\parallel BX\,$ and $AC=\varphi\cdot BX.\,$ By Thales' Theorem, $\displaystyle\frac{AS}{SX}=\frac{CS}{SB}=\varphi.$
Solution 2
We'll start with angle chasing.
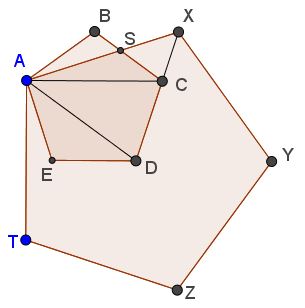
$\angle DAE=36^{\circ},\,$ $\angle DAT=54^{\circ},\,$ hence $\angle SAB=\angle EAT=18^{\circ}.\,$ Since $\angle CAB=36^{\circ},\,$ $\angle CAS=18^{\circ},\,$ such that $AS\,$ is an angle bisector in $\Delta BAD.\,$ By a property of angle bisectors, $\displaystyle\frac{AC}{AB}=\frac{CS}{SB}.\,$ Since the former is $\varphi,\,$ so is the latter.
$\begin{align}\angle CSX&=\angle ASB=180^{\circ}-\angle ABC-\angle SAB\\ &= 180^{\circ}-108^{\circ}-18^{\circ}\\ &=54^{\circ}. \end{align}$
$\angle AXD=54^{\circ}\,$ and $\angle BCD=108^{\circ},\,$ so that $\angle SCX=180^{\circ}-2\cdot 54^{\circ}=72^{\circ}\,$ is supplementary to $\angle BCD,\,$ which makes $D,C,X\,$ colinear.
$\Delta ABX\,$ is obtained by rotating $\Delta AET\,$ counterclockwise through $108^{\circ}.\,$ Thus, $\angle BXA=\angle AET=18^{\circ}=\angle CAS,\,$ implying $BX\parallel AC\,$ and making triangles $ACS\,$ and $XBS\,$ similar. In particular, $\displaystyle\frac{AS}{SX}=\frac{CS}{SB}=\varphi.$
Acknowledgment
The problem has been kindly posted at the CutTheKnotMath facebook page by Tran Quang Hung. Solution 1 is by Leo Giugiuc.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73604118
