Geometrical Exploits

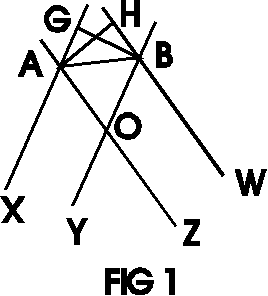
Lemma 1.

Given two pairs of parallel lines - (XA,YB) and (ZA,WB), see FIG 1. Assume that distances between the lines in the two pairs are equal, i.e., dist(XA, YB) = dist(ZA, WB). Then

1. ∠XAB = ∠ABW
2. OA = OB.

Proof:

Let us drop perpendiculars from A and B onto WB and XA, respectively. Two right triangles ABH and ABG are equal. Indeed, they share a hypotenuse AB and AH = BG by the conditions of the Lemma. Therefore, ∠GAB = ∠HBA. However, ∠XAB = 180 - ∠GAB and ∠ABW = 180 - ∠HBA. Which proves 1.
Further, ∠XAZ = ∠YBW since their sides are parallel. Subtracting this from 1 we get ∠OAB = ∠OBA so that the triangle OAB is isosceles. This proves 2.
Now referring to FIG 2. we have the following

Corollary 1.

1. ∠EAB = ∠ABC = ∠BCD.
2. ∠CDE = ∠DEA.

Corollary 2.

EA = AB = BC = CD.

Indeed, each of the above segments serves as a hypotenuse of a right triangle built in the manner of ABH and ABG on FIG 1.

Corollary 3.

AD = BE.

Indeed, by Lemma 1.2 AD = BD and BD = BE.

Lemma 2.

Two quadrilaterals ABCD and BCDE are equal.

Proof:

Both quadrilaterals are trapeze. We sum up equality of their corresponding elements in the following table:

ABCD BCDE reason

∠ABC equals ∠BCD by Corollary 1
AB equals BC by Corollary 2
BC equals CD by Corollary 2
AD equals BE by Corollary 3

Q.E.D.

Corollary 4.

1. CD = DE.
2. ∠BCD = ∠CDE

Now combining Corollaries 1, 2 and 4 we obtain, as promised, the following

Theorem.

ABCDE on FIG 2 is a regular pentagon.

72365459