Golden Ratio via Golden Rhombus

John Molokach came up with a construction of the golden ratio by first constructing a golden rhombus, that is, a rhombus in which the ratio of the diagonals (long to short) equals φ.

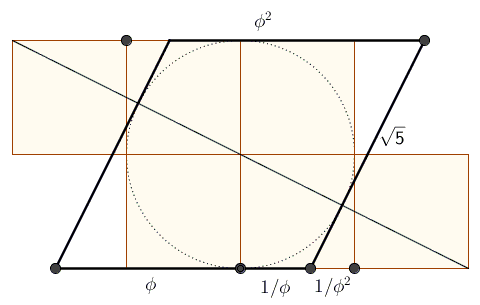
In one sweep, John additionally obtains 1/φ, 1/φ², and φ². How does this work?

Put together two $1\times 3$ rectangles shifted one unit relative to each other, as shown above. Draw the long diagonal of the resulting shape and the unit circle at its center. Draw the tangents to the circle at the points where it meets the diagonal. All sides of the obtained quadrilateral equal $\sqrt{5},$ so this is indeed a rhombus.

Draw its (perpendicular) half-diagonals to obtain a right triangle $ABC$ with the altitude $CH,$ as shown below.

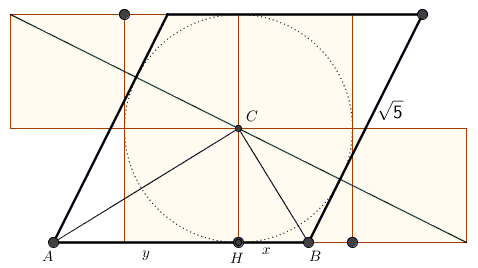
From the two equations $x+y=\sqrt{5}$ and $xy=1$, $\displaystyle x=\frac{\sqrt{5}-1}{2}=\frac{1}{\phi}$ and $\displaystyle y=\frac{\sqrt{5}+1}{2}=\phi.$

Now, $\displaystyle\bigg(\frac{AC}{BC}\bigg)^2=\frac{y^{2}+1}{x^{2}+1}=\frac{\phi^{2}+1}{(1/\phi)^{2}+1}=\phi^2$ which shows that the diagonals in the rhombus are indeed in the Golden Ratio.

Further, $\displaystyle 1-\frac{1}{\phi}=\frac{1}{\phi^2}$ because $\phi^2-\phi-1=0,$ while

\(\displaystyle \begin{align} \sqrt{5}+\frac{1}{\phi^2}&=\sqrt{5}+\frac{5-2\sqrt{5}+1}{4} \\ &=\frac{2\sqrt{5}+6}{4} \\ &=\bigg(\frac{\sqrt{5}+1}{2}\bigg)^2\\ &=\phi^2. \end{align} \)

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny