Cultivating Regular Pentagons
Problem
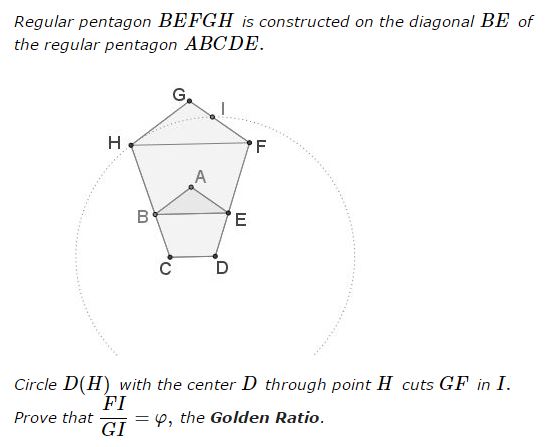
Solution 1
First note that, being an isosceles trapezoid, $CDFH\,$ is cyclic. Let $I'\,$ be the point where circle $(CDFH)\,$ meets $FG.$
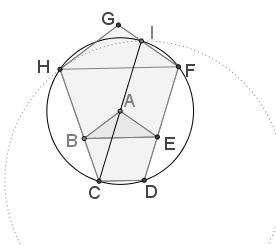
In the regular pentagon $ABCDE,\,$ $AC\parallel DE,\,$ and let the extension of $AC\,$ cross $FG\,$ in $I''.\,$ We'll show that $I'=I''=I.$
Trapezoid $CDFI''\,$ is isosceles, hence, cyclic. $(CDFI'')=(CDF)=(CDFH)\,$ from which $I''=I'.\,$ Further, in the isosceles trapezoid $CDFI''\,$ $CF=DI'';\,$ in the isosceles trapezoid $CDFH\,$ $CF=DH.\,$ By transitivity, $DI''=CF=DH,\,$ such that $I''\in D(H)\,$ and, subsequently, $I''=I.$
To solve the original problem, suffice it to note that $AC\,$ divides $BE\,$ in the golden ratio. Thus, by Thales' theorem, it is also true for $FG:$
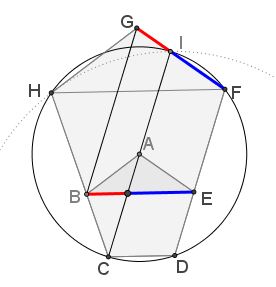
Solution 2
Let $\beta=72^o\,$ and the side of the smaller pentagon be $p.\,$ Let $\displaystyle k=\frac{\varphi}{1+\varphi}.$
The side of the larger pentagon is then $q=2p\cos(\beta/2).\,$ With origin at $D\,$ and the $X\,$ axis parallel to $CD,\,$ the coordinates of the relevant points are:
$\displaystyle \begin{align} F&\rightarrow \left((p+q)\cos\beta,(p+q)\sin\beta\right), \\ H&\rightarrow \left(-p-(p+q)\cos\beta,(p+q)\sin\beta\right), \\ G&\rightarrow \left((p+q)\cos\beta+q\cos 2\beta,(p+q)\sin\beta+q\sin 2\beta\right), \\ I&\rightarrow \left((p+q)\cos\beta+kq\cos 2\beta,(p+q)\sin\beta+kq\sin 2\beta\right). \end{align}$
Both, $H\,$ and $I\,$ being on the circle centered at $D\,$ means
$\displaystyle \begin{align} &|I|^2=|H|^2 \\ &[(p+q)\cos\beta+kq\cos 2\beta]^2+[(p+q)\sin\beta+kq\sin 2\beta]^2 = \\ &\qquad\qquad\qquad[-p-(p+q)\cos\beta]^2+[(p+q)\sin\beta]^2 \\ &k^2q^2+2kq(p+q)\cos\beta-p^2-2p(p+q)\cos\beta=0 \\ &4k^2\cos^2\left(\frac{\beta}{2}\right)+4\cos\left(\frac{\beta}{2}\right)k\left[1+2\cos\left(\frac{\beta}{2}\right)\right]\cos\beta-1 \\ &\qquad\qquad\qquad-2\left[1+2\cos\left(\frac{\beta}{2}\right)\right]\cos\beta=0 \end{align}$
Plugging in the values:
$\displaystyle \begin{align} \cos\left(\frac{\beta}{2}\right)&= \cos~36^o=\frac{\sqrt{5}+1}{4} \\ \cos\beta&= \cos~72^o=\frac{\sqrt{5}-1}{4}, \end{align}$
gives
$\displaystyle 2(\sqrt{5}+3)k^2+(\sqrt{5}+1)^2k-2(\sqrt{5}+3)=0$
with roots
$\displaystyle k=\left\{\left(\frac{\sqrt{5}-1}{2}\right),-\left(\frac{\sqrt{5}+1}{2}\right)\right\}.$
Choosing the physical root,
$\displaystyle \begin{align} \frac{\varphi}{1+\varphi}&= \frac{\sqrt{5}-1}{2}, \\ \varphi&= \frac{\sqrt{5}+1}{2}. \end{align}$
Extension
We may continue building a pyramid of regular pentagons, as shown below:
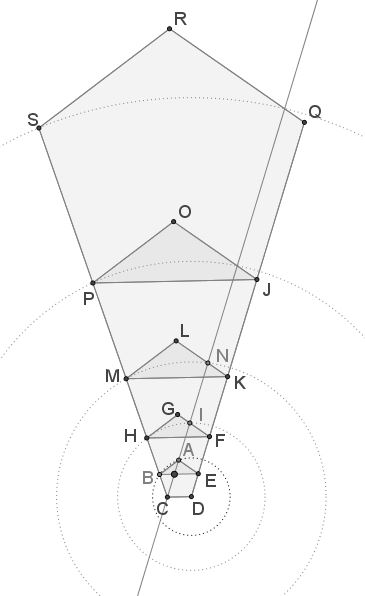
As above, the circles $D(M),\,\,$ $D(P),\,\,$ $D(S),\,\,$ etc., meet $AC\,\,\,$ on the sides of the corresponding pentagons. If $N=AC\cap KL=D(M)\cap KL,\,\,$ then $\displaystyle \frac{LN}{KN}=\varphi,\,\,$ the Golden Ratio.
Acknowledgment
The problem has been kindly posted by Tran Quang Hung at the CutTheKnotMath facebook page. GeoGebra made it easy to draw and investigate the construction. Solution 2 is by Amit Itagi.
Golden Ratio
- Golden Ratio in Geometry
- Golden Ratio in Regular Pentagon
- Golden Ratio in an Irregular Pentagon
- Golden Ratio in a Irregular Pentagon II
- Inflection Points of Fourth Degree Polynomials
- Wythoff's Nim
- Inscribing a regular pentagon in a circle - and proving it
- Cosine of 36 degrees
- Continued Fractions
- Golden Window
- Golden Ratio and the Egyptian Triangle
- Golden Ratio by Compass Only
- Golden Ratio with a Rusty Compass
- From Equilateral Triangle and Square to Golden Ratio
- Golden Ratio and Midpoints
- Golden Section in Two Equilateral Triangles
- Golden Section in Two Equilateral Triangles, II
- Golden Ratio is Irrational
- Triangles with Sides in Geometric Progression
- Golden Ratio in Hexagon
- Golden Ratio in Equilateral Triangles
- Golden Ratio in Square
- Golden Ratio via van Obel's Theorem
- Golden Ratio in Circle - in Droves
- From 3 to Golden Ratio in Semicircle
- Another Golden Ratio in Semicircle
- Golden Ratio in Two Squares
- Golden Ratio in Two Equilateral Triangles
- Golden Ratio As a Mathematical Morsel
- Golden Ratio in Inscribed Equilateral Triangles
- Golden Ratio in a Rhombus
- Golden Ratio in Five Steps
- Between a Cross and a Square
- Four Golden Circles
- Golden Ratio in Mixtilinear Circles
- Golden Ratio With Two Equal Circles And a Line
- Golden Ratio in a Chain of Polygons, So to Speak
- Golden Ratio With Two Unequal Circles And a Line
- Golden Ratio In a 3x3 Square
- Golden Ratio In a 3x3 Square II
- Golden Ratio In Three Tangent Circles
- Golden Ratio In Right Isosceles Triangle
- Golden Ratio Poster
- Golden Ratio Next to the Poster
- Golden Ratio In Rectangles
- Golden Ratio In a 2x2 Square: Without And Within
- Golden Ratio With Two Unequal Circles And a Line II
- Golden Ratio in Equilateral and Right Isosceles Triangles
- Golden Ratio in a Butterfly Astride an Equilateral Triangle
- The Golden Pentacross
- 5-Step Construction of the Golden Ratio, One of Many
- Golden Ratio in 5-gon and 6-gon
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle
- Golden Ratio in Pentagon And Two Squares
- Golden Ratio in Pentagon And Three Triangles
- Golden Ratio in a Mutually Beneficial Relationship
- Star, Six Pentagons and Golden Ratio
- Rotating Square in Search of the Golden Ratio
- Cultivating Regular Pentagons
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle II
- More of Gloden Ratio in Equilateral Triangles
- Golden Ratio in Three Regular Pentagons
- Golden Ratio in Three Regular Pentagons II
- Golden Ratio in Wu Xing
- Golden Ratio In Three Circles And Common Secant
- Flat Probabilities on a Sphere
- Golden Ratio in Square And Circles
- Golden Ratio in Square
- Golden Ratio in Two Squares, Or, Perhaps in Three
- Golden Ratio in Isosceles Triangle
- Golden Ratio in Circles
- Golden Ratio in Isosceles Triangle II
- Golden Ratio in Yin-Yang
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73604444
